Σ ⇒ φ to mean that the premises in set Σ non-monotonically entail sentence φ.
Other texts will write that like this: 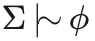 .
.We’re going to shift away now from modal representations of knowledge and belief to a group of interconnected systems going by names like “non-monotonic logics,” “belief revision frameworks,” and so on. A prominent such system, that we’ll mostly focus on, is called the AGM framework — we’ll explain it below. As we exposit these systems, we’ll try to get you to appreciate five major limits, at least in the core systems. (There is some work towards next-generation systems that suffer less in some ways from some of these limits, but those systems are more controversial and more complicated. We’re not going to explore them in this course, but we’ll tell you a bit about how some of them get started.) Limits are just things that these systems cannot do, but arguably should not be understood as aiming to do, either. In addition to these limits, in our second session, we’ll also be exploring four doubts about or challenges to fundamental choices these systems make. These question how good a job the systems do in their declared aims.
As we transition from modal systems into this next group, let’s note what the major differences will be. The new systems will gain some new expressive powers, but at the same time will lose others.
One feature of modal systems is that they express epistemic/doxastic facts in the very object language — with □φ perhaps meaning agent so-and-so knows/is in a position to rationally believe
We may also have different varieties of φ.□, e.g. for different agents, or reporting what is known after different facts have been announced.
Our initial exposition of modal systems was concerned only with that an agent knows or believes at a single time, on the basis of a single body of evidence. But when looking at applications, we shifted to considering systems that tried to model how the agent’s state evolved as new information came in. We said that it’s the overwhelming norm for these systems to represent learning always as a matter of ruling more epistemic possibilities out.
The new systems we’re turning to now will lose the expressive power of feature #1 (this will be their first major limit), but they will gain the ability to model other kinds of learning, where an agent withdraws beliefs they formed earlier, and so lets some epistemic possibilities back in.
However, these systems only attempt to model evolving information and beliefs about a static, unchanging world. This is their second major limit. Because of the first limit, their inability to represent and manipulate claims about the agent’s information and beliefs, they won’t model evolving information and beliefs about that, either. (Contrast our application of modal systems to the muddy children puzzle.)
Classical deductive consequence, and many extensions and variations on that studied by logicians, are determined by logical structure. Thus the first of these displays something that is a logical consequence, but the second displays something that isn’t:
The cage contains a bird ⊨ The cage contains something.The cage contains a bird ⊭ The cage contains an animal.The inference mentioned on the second line would depend on the specific meanings of “bird” and “animal,” and so on more than just the logical structure of the sentences. Whereas the relation between “a bird” and “something” is understood to be determined just by the sentences’ syntax and the logical role of “something.”
Ordinary good reasoning is sensitive to meanings as well as to logical structure, and so would endorse the second inference too. It would also endorse many cases of inference that are only defeasibly good, such as:
The cage contains a bird. Therefore the cage contains something that can fly.That inference is a reasonable one, given only the information listed in its premises. But it would be possible to learn more premises, that don’t change our mind about the cage containing a bird, but make the conclusion no longer seem reasonable:
Here the expanded set of premises makes it more plausible that the bird is a penguin, in which case it cannot fly. Inferences like these are called non-monotonic or defeasible, because they can be good on the basis of one body of evidence, without also being good on the basis of every expanded body of evidence.
Recall in some earlier webnotes, we discussed three characteristics that logical consequence relations standardly have:
For any formula Q, Q ⊨ Q.
For all sets of formulas Δ and Γ, if Γ ⊨ D for every D ∈ Δ, and Γ, Δ ⊨ Q, then also Γ ⊨ Q.
For all sets of formulas Δ and Γ, if Γ ⊨ Q, then also Γ, Δ ⊨ Q.
Γ is identical to the set of consequences of consequences of Γ. Sometimes Monotonicity will be formulated with single sentences instead of sets of sentences, for example as:If Γ ⊨ Q then Γ, D ⊨ Q
If G ⊨ Q then G ∧ D ⊨ Q
Often these are just stylistic choices, but there can be contexts in which the subtle choices between these matter. However, we’re working with broad brushstrokes here and won’t try to track those fine details.
If we designate the set of deductive consequences of Γ as Cn(Γ), then another way to express Monotonicity would be like this (with Θ playing the role of Γ ∪ Δ):
If Γ ⊆ Θ then Cn(Γ) ⊆ Cn(Θ)
Our example with the bird in a cage that later premises suggest may be an unflying Antarctic penguin shows that the kinds of inference we’re taking up now will give up Monotonicity. Let’s use a different symbol to represent that we’re dealing with non-monotonic consequence, that is, with inferences that want to be evaluated by standards other than whether they’re deductively valid.
Some texts will write Σ ⇒ φ to mean that the premises in set Σ non-monotonically entail sentence φ.
Other texts will write that like this: 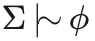 .
.
Σ ƕ φ
Nonmonotonic entailments are thought to also be Reflexive and to satisfy a Cut-like principle, but not to satisfy Monotonicity. Thus, theorists won’t assume that when Γ ƕ Q, it always holds that Γ, Δ ƕ Q. In place of such a Monotonicity principle, systems that use non-monotonic consequence relations will often endorse this much weaker claim:
For all sets of formulas Δ and Γ, if Γ ƕ D for every D ∈ Δ, and Γ ƕ Q, then also Γ, Δ ƕ Q.
This postulate is something like the converse of Cut, and is very widely accepted. Cut and Cautious Monotonicity together capture the intuitive idea that if you add to a theory Γ some of its own consequences Δ, what is supported should be exactly the same.
There’s also another alternative, which is stronger than Cautious Monotonicity but weaker than full Monotonicity:
For all sets of formulas Δ and Γ, if Γ ƕ̸ ¬D for every D ∈ Δ, and Γ ƕ Q, then also Γ, Δ ƕ Q.
Although this postulate is substantially more controversial than Cautious Monotonicity, accepting Rational Monotonicity (along with Cautious Monotonicity, which it entails) is more popular than accepting Cautious Monotonicity alone. We’ll mostly be thinking about systems that do validate Rational Monotonicity, though we will also later be considering some arguments against it.
One very weak and widely endorsed set of postulates for non-monotonic consequence are the following. They are called System P or the KLM postulates (for a 1990 paper by Kraus, Lehmann, and Magidor):
Q ƕ QG ƕ D and G ∧ D ƕ Q, then G ƕ QG ƕ D and G ƕ Q, then G ∧ D ƕ QG ƕ Q and D ƕ Q, then G ∨ D ƕ QP ⊃ Q, and also G ƕ P, then G ƕ QP ⊂⊃ Q, and also P ƕ G, then Q ƕ GTwo derived rules of this system are:
G ƕ D and G ƕ Q, then G ƕ D ∧ QG ∧ D ƕ Q, then G ƕ D ⊃ QThe idea behind these systems is not that they characterize a single correct or reasonable consequence relation ƕ. Rather, they aim to state constraints that any of the many reasonable such consequence relations would have to respect. It’s expected that you and I might have reasonably different ƕs that entail different (even incompatible) conclusions, on the basis of the same initial evidence G. (Or, if there are facts that make your ƕ the uniquely rational one, they’ll have to go beyond the less restrictive constraints proposed in these systems.)
System P is not the absolutely weakest set of postulates that have been proposed, but most systems that are studied and discussed are strengthenings of System P.
One system that will be important below is called System R, and this just adds the postulate of Rational Monotonicity to System P.
If it’s a deductive theorem that P ⊃ Q, then ⊨ □P ⊃ □Q
Note the similar Postulate 5 in System P for ƕ. These postulates incorporate assumptions of logical omniscience, and this is the third major limit of the systems we’re looking at.
It’s possible to re-frame System P and related systems in terms of an “ordering relation” on possible worlds
(in a manner that’s similar, but also different in some ways, to the role that ordering relations on possible worlds play in Lewis’ and Stalnaker’s semantics for counterfactuals).
The idea is that agents order their open epistemically accessible possibilities in terms of how surprising/unexpected they would be. The least surprising possibilities where G is true are called the agent’s most plausible or normal
Then if for me, G worlds.G ƕ D, that means that D is true in all my most normal G worlds.
Re-framed in that way, the constraints of System P enforce that one’s “more normal” relation on worlds be a certain kind of preorder.
The stronger System R (that adds in Rational Monotonicity) adds the requirement that all worlds are comparable for normality (always either u ⊑ v or v ⊑ u), so “more normal” will be a total preorder.
Belief revision frameworks start with some representation of what you currently accept or believe. Conventionally these representations are labeled 𝓚 or 𝓑. I’ll use the former.
These systems then make proposals about what you should accept after learning some new sentence A. They represent that new acceptance/belief state as 𝓚 ★ A. (Sometimes you might see that written as 𝓚 ⊛ A or in other ways.) And then what you should accept after learning a further sentence B would be (𝓚 ★ A) ★ B, which you’ll also see written without the parentheses.
The label 𝓚 should not be construed as meaning we’re talking about things the agent knows — some of what they accept or believe, including the new sentences they learn, can be false.
As with ƕ, it’s not expected that there will be a single correct or reasonable strategy for revising one’s acceptances/beliefs. If you and I start in the same initial state 𝓚, and both learn A, you may reasonably change to state 𝓚 ★₁ A while I reasonably change to state 𝓚 ★₂ A, where these new acceptance/belief states are different. All the belief revision frameworks aim to do is to identify constraints on reasonable revision functions ★i. Usually we’ll only be talking about one such function at a time, and so we leave the subscripts off.
We can move back and forth between talking of a non-monotonic consequence relation ƕ and a belief revision framework. (Here we assume, as we will below, that acceptance/belief states are just sets of sentences.)
ƕ, one can define 𝓚 := {Q | ⊤ ƕ Q}, and define 𝓚 ★ A := {Q | A ƕ Q}.𝓚 and ★, one can define A ƕ Q := Q ∈ 𝓚 ★ A. (Note that this gives a different ƕ for each choice of K and ★. So even for a single agent, this ƕ will change every time they revise what they accept or believe.)The main belief revision framework we’ll be considering, AGM, turns out to be equivalent to using a ƕ that obeys System R, that is, the strengthening of System P that adds in Rational Monotonicity.
One last preliminary. Note that claims like A ƕ Q are claims in our metalanguage about what inferences between sentences in the object language are appropriate or validated or good. We haven’t yet discussed what the object language itself looks like. In particular, we haven’t said whether claims like A ƕ Q, or anything corresponding to that, can themself be part of the object language. There will turn out to be severe difficulties and limitations to allowing that. This is part of the first major limit of these systems, that we mentioned before.
The AGM belief revision system has its roots in work done by Levi and by Harper in the 1970s, but became prominent and got its name from a 1985 paper by Alchourrón, Gärdenfors, and Makinson.
Their representation 𝓚 of an agent’s acceptance/belief state is just a set of sentences closed under deductive entailment (⊨). They call these belief sets.
Later we’ll see some ways in which this representation is incomplete, and mention some extensions and nearby alternatives.
The AGM Postulates lay down constraints on reasonable revision functions ★, in the way that Systems P and R lay down constraints on reasonable non-monotonic consequence relations ƕ.
Let’s consider a list of 9 such postulates, divided into three groups.
The first group consists of mainly synchronic constraints on the outputs of belief revision function:
𝓚 ★ A = Cn(𝓚 ★ A), where Cn(Γ) is the set of deductive consequences of Γ. FIXMEA ⊂⊃ B, then 𝓚 ★ A = 𝓚 ★ B𝓚 ★ A is inconsistent (so, given Closure, contains every sentence in the language), then either A was inconsistent (⊨ ¬A) or 𝓚 was. (Often presentations of AGM omit the second alternative, in effect requiring that whenever an inconsistent 𝓚 is revised with any consistent sentence, even ⊤, consistency gets restored.)A ∈ 𝓚 ★ A. This says that the newly learned sentence always gets included in the new belief set. It entails that when one “learns” an inconsistent A, the resulting state 𝓚 ★ A must then also be inconsistent.Note that Closure (like Postulate 5 in System P) builds in an assumption of logical omniscience. In a different way, so too does the above Postulate 2. We’re calling these assumptions the the third major limit of these frameworks.
The second group of postulates consists of two diachronic constraints, about how 𝓚 ★ A relates to 𝓚. (Perhaps some of the previous group could also be described that way, but trust us it will be useful to have these two postulates separate.)
𝓚 ★ A ⊆ Cn(𝓚 ∪ {A})A is consistent with the sentences in 𝓚 (that is, ¬A ∉ 𝓚), then 𝓚 ⊆ 𝓚 ★ A. (Sometimes this is instead called “Vacuity,” and often its consequence is formulated instead as Cn(𝓚 ∪ {A}) ⊆ 𝓚 ★ A. Given the other AGM Postulates, these two formulations have the same effect.)Postulate 6 tells us that when you learn an A that’s consistent with what you already accept, you shouldn’t lose any sentences from your initial state 𝓚. You may and usually will gain some sentences. Together with Postulate 5 we see that your new state should exactly be the deductive closure of your old belief set’s union with {A}.
The third group of postulates impose some constraints on how revisions by A and by B should be related to revisions by their logical combinations:
𝓚 ★ (A ∧ B) ⊆ Cn((𝓚 ★ A) ∪ {B})B is consistent with the sentences in 𝓚 ★ A, then 𝓚 ★ A ⊆ 𝓚 ★ (A ∧ B). (As with the earlier Preservation Postulate 6, the consequence of this is often formulated instead as Cn((𝓚 ★ A) ∪ {B}) ⊆ 𝓚 ★ (A ∧ B). Given the other AGM Postulates, these two formulations again turn out to be equivalent.)𝓚 ★ (A ∨ B) must be one of 𝓚 ★ A, 𝓚 ★ B, or (𝓚 ★ A) ∩ (𝓚 ★ B)It turns out that adding Postulates 7 and 8 to the first six is equivalent to adding (only) Postulate 9.
Postulates 7 and 8 look like applications of Postulates 5 and 6 to an initial belief set of 𝓚 ★ A, with the newly learned information now being B. The difference is that where the latter would refer to (𝓚 ★ A) ★ B, the former instead refers to 𝓚 ★ (A ∧ B).
In different texts you’ll see minor variations in how these postulates are presented. Compare Sturgeon’s Revision Postulates (*1) through (*8). His Postulate (*1) says that 𝓚 ★ A is always (a) consistent and (b) “fully logical.” By (b) he means our Closure Postulate 1. Sturgeon’s claim (a) is correct only when A itself is consistent, which he seems to be silently assuming there. Sturgeon’s Postulate (*5) is our Consistency Postulate, albeit Sturgeon also includes a redundant “if” (the “if” direction is already entailed by the Success Postulate). Sturgeon’s Postulate (*4) is our Preservation Postulate 6, with the alternative consequent and using an abbreviation common to this literature, where Cn(𝓚 ∪ {A}) is written as 𝓚 + A. Ditto for the And-Preservation Postulates. Sturgeon’s other Postulates are the same as the rest of our first 8.
As we said, our AGM Postulates 5 (Inclusion) and 6 (Preservation) have the combined effect that, when the sentence you learn is consistent with what you already accept, you retain everything you already accept/believe, and just add in the new sentence, plus any new deductive consequences of all those taken together. (This “easy” form of revision is referred to as expanding your belief set.)
What if the new sentence does conflict with what you already accept? Let’s assume your prior beliefs are consistent among themselves, and the new sentence A is also consistent, but among the prior beliefs is ¬A. In this case, something has to yield, and the Success Postulate 4 tells us it’s not the new sentence that should yield, so it must instead be some of your prior beliefs. (We’ll discuss later whether it’s right to require that the tension always be resolved in this way.) At least your prior belief ¬A must be withdrawn, but also beliefs that entail it. There may be more than one choice about how to achieve that.
For example, if your belief set also contains B and ¬(B ∧ A), you could withdraw either one (or both) of these further beliefs.
In addition to talking about revision functions ★, the AGM literature also talks about contraction functions. 𝓚 ⊖ ¬A represents the result of an initial state 𝓚 after withdrawing ¬A in some reasonable way — so also including any sentences that entail ¬A. You may also see this written as:
𝓚 - ¬A
𝓚 ∸ ¬A
𝓚 ÷ ¬AAs with revision functions, it’s also expected there will be multiple reasonable contraction functions. The AGM literature discusses postulates for these in the same way it does for ★. (See Sturgeon’s Contraction Postulates (–1) through (–8).) We want to call attention to one of these postulates in particular, usually called:
𝓚 ⊆ Cn((𝓚 ⊖ A) ∪ {A})
This is Sturgeon’s (–5). What it implies is that if you withdraw A but then again learn A, you should always end up having (at least) the acceptances/beliefs that you started with.
We also want to call attention to strategies where, if you’re given one of a ★ or a ⊖, you can use it to define the other:
𝓚 ★ A := Cn((𝓚 ⊖ ¬A) ∪ {A})
𝓚 ⊖ C := 𝓚 ∩ (𝓚 ★ ¬C)
It turns out that, if you take some contraction function satisfying all of the proposed Contraction Postulates, with the possible exception of Recovery, and use the Levi Identity to define a revision function ★ in terms of it, what you get will satisfy all the AGM Postulates on ★ we listed above. More than one contraction function will map to the same ★, but if you then take that ★ and use the Harper Identity to derive the corresponding ⊖, it will be the single one of those that satisfies Recovery. So we can take that ⊖ as being the official or canonical contraction function paired with that revision function ★.
These paired ⊖ and ★ are two faces of a single reasonable strategy for revising the sentences you accept/believe. When a new sentence A you learn is compatible with your existing 𝓚, you just expand your belief set to include it, as we discussed, without withdrawing any old acceptances/beliefs. When it’s incompatible, you withdraw ¬A using ⊖, and then just add A (plus any new consequences) to the resulting, now-compatible-with-A state 𝓚 ⊖ ¬A.
There will be multiple ways to contract that respect the relevant postulates on ⊖, corresponding to there being multiple ways to revise that respect our AGM Postulates on ★.
One way to contract would be:
C ∉ 𝓚, then 𝓚 ⊖ C is just 𝓚. That is, you don’t need to withdraw things you didn’t already accept.C is a deductive theorem, then 𝓚 ⊖ C is just 𝓚. That is, you don’t withdraw your acceptance of theorems.𝓚 ⊖ C is Cn(∅). That is, you contract by giving up all your prior accepted/believed sentences (except for theorems).Call this the extremely timid contraction strategy. It’s intuitively unattractive, but may be allowed by the AGM framework. Fortunately, other intuitively more reasonable contraction strategies are allowed as well.
The way these strategies are discussed in the AGM literature is this.
You’re in state 𝓚 and want to contract by sentence C. We start with all of the maximal subsets of 𝓚 that don’t entail C. The set of these is written as 𝓚 ⊥ C, pronounced
or 𝓚 remainder Cremainders of
Each element 𝓚 without C.J of this set is a subset of 𝓚 that does not entail C, and such that there is no J+ where J+ also does not entail C and J ⊂ J+ ⊆ 𝓚. That is, the Js are different ways of minimally shrinking 𝓚 to remove its commitment to C. It’s assumed that the agent has some way of ordering these Js according to which they count as “better” ways of so shrinking 𝓚. If there are multiple Js that come out “best” by the agent’s lights, then the agent adopts the intersection of those Js as their new belief set — that is, their new state accepts just those sentences that are included in all of their “best” ways J of minimally shrinking their prior belief set to remove its commitment to C. This is called a partial meet contraction strategy.
(“Meet” refers to the intersecting, and this is “partial” because it only uses the Js the agent counts as “best.”)
The only time when there will be no Js in 𝓚 ⊥ C to apply this strategy to is when C is a deductive theorem. In that case the framework says the agent should just stay with 𝓚.
An important result in the AGM literature is that any such contraction strategy will satisfy the proposed postulates on contraction (including Recovery)
that correspond to our AGM Postulates 1–6 on ★. (To also secure AGM Postulates 7–9, you need to impose more constraints.)
The converse is also true: for any ★ satisfying AGM Postulates 1–6, there will be a way of selecting which Js are “best” such that the partial meet contraction strategy delivers the paired ⊖.
Instead of the agent counting some sets in 𝓚 ⊥ C as “better” than others, here’s another way to theorize about how the operation 𝓚 ⊖ C should work.
(These ideas will turn out in the end to give the same results.)
We assume that the agent has an ordering on individual sentences, that we will write as A ⊑ B and pronounce as
.
(Some texts, including Sturgeon pp. 171–3, talk about “how entrenched” sets of sentences are; but the notion we’re working with here is a relation between individual sentences.)
This entrenchment ordering has the whole language as its domain, and depends on the agent’s current state — when they revise what they accept or believe, they should be expected to change their entrenchment ordering.
These orderings are assumed to obey certain constraints:A is less or equally entrenched as B
A ⊃ B, then A ⊑ BConstraint 2 implies tha the relation is reflexive, and hence together with Constraint 1, that it’s a preorder. Continuing:
A ⊑ (A ∧ B) or B ⊑ (A ∧ B)We already know from Constraint 2 that A ∧ B can’t be more entrenched than either A or B; what Constraint 3 tells us is that it will be at least as entrenched as one of them. These first three Constraints together imply that ⊑ is a total preorder.
If we define:
A ⊏ B := A ⊑ B ∧ ¬(A ⊒ B)then ⊑ being a total preorder implies that A ⊏ B iff ¬(A ⊒ B). Continuing:
B is a greatest element for ⊑ (that is, every sentence in the language is ⊑ B), then B is a deductive theoremBy itself this leaves open the possibility that some deductive theorems are non-greatest, or that there’s an infinitely ascending chain of sentences, with none greatest. But Constraints 4 and 2 together imply that all and only deductive theorems will be greatest. Continuing:
𝓚 is consistent, then 𝓚 = {Q | ∃P. P ⊏ Q}This says that all and only the minimally entrenched sentences fail to be ∈ 𝓚. Hence, given a ⊑ we can derive the 𝓚 it’s paired with.
Given an entrenchment ordering satisfying these conditions, a contraction function can be generated like so:
𝓚 ⊖ C := {Q ∈ K | C is a deductive theorem or C ⊏ (C ∨ Q)}
It turns out that any contraction function generated in this way will satisfy the proposed postulates on contraction that correspond to AGM Postulates 1–9. The converse is also true: given a ★ satisying the postulates, a ⊑ exists from which the paired ⊖ can be so generated.
For purposes of our later discussion, let’s emphasize here something we’ve seen in the preceeding: given a choice of some 𝓚, there will be multiple pairs of ★ and ⊖ that the AGM Postulates admit as reasonable. So an agent’s ★ and ⊖ can’t be “read off” from their 𝓚. To see what their belief set will be after contracting by C, except for a few special choices of C, we need to look at something more specific than their 𝓚, such as what remainder sets in 𝓚 ⊥ C the agent counts as “best,” or what their current entrenchment ordering on sentences is, or we can inspect their ⊖ directly. The answer won’t in general be present in the prior belief set 𝓚 itself.
An impressive fact about these systems is how many equivalences have been established between them — not just between the AGM Postulates for ★ (which we listed) and for ⊖ (which we’ve only here reproduced some of), but also between these and System R for non-monotonic consequence, and between each of these and natural ways of ordering possible worlds as “more plausible or normal,” or sentences as “more entrenched.” So the theoretical strengths of these systems go considerably beyond what intuitive motivations can be given for each of their postulates individually.
Nonetheless, there are important things these systems cannot do — what we’re calling their “five major limits” — and also reasons to doubt or question whether they even do correctly what they aim to do. We’ll discuss four of these (more are raised in the literature, we’re not aiming for an exhaustive survey).
We’ve mentioned three of their limits so far:
Here we’ll briefly expand on the first of these. (We’ll describe the fourth and fifth limits, and all four of the doubts we want to discuss, in our next session.)
Let’s see what happens if we try to add to these frameworks the ability to have sentences that describe (instead of merely contributing to) the agent’s own state.
Consider a hypothetical sentence ◊A, which is meant to be ∈ 𝓚 iff ¬A ∉ 𝓚. Let’s start with an initial 𝓚 that does include ¬A; hence 𝓚 will not include ◊A. Now let’s contract by ¬A. It’s clear from the Harper Identity that any 𝓚 ⊖ C will be ⊆ 𝓚, and indeed this is one of the postulates for ⊖. It follows that 𝓚 ⊖ ¬A cannot include ◊A either. But this conflicts with the intended meaning of ◊A.
Notice, the issue isn’t that the framework merely so far fails to provide any such ◊A. It’s worse: the framework’s postulates conflict with there being sentences with the desired behavior.
Another kind of sentence it’d be desirable to have in the framework would be a conditional P ⤳ Q, which is meant to be ∈ 𝓚 iff Q ∈ (𝓚 ★ P). Such a conditional aims to capture what Ramsey described:
If two people are arguing
If P will Q?and are both in doubt as to P, they are adding P hypothetically to their stock of knowledge and arguing on that basis about Q… (quoted on Sturgeon p. 176)
Such a conditional could be interpreted as saying something like If
or P then likely QP will be a prima facie reason to accept Q.
Here, too, there are obstacles to including sentences that work this way in frameworks like AGM. Gärdenfors proved that sentences with this behavior constrain the AGM Postulates to allow only unattractive contraction functions, like the extremely timid one we described before. So giving a framework this kind of ability to describe its own prospective revisions will require rejecting some of those postulates. There is work exploring how best to do this, but so far no consensus.