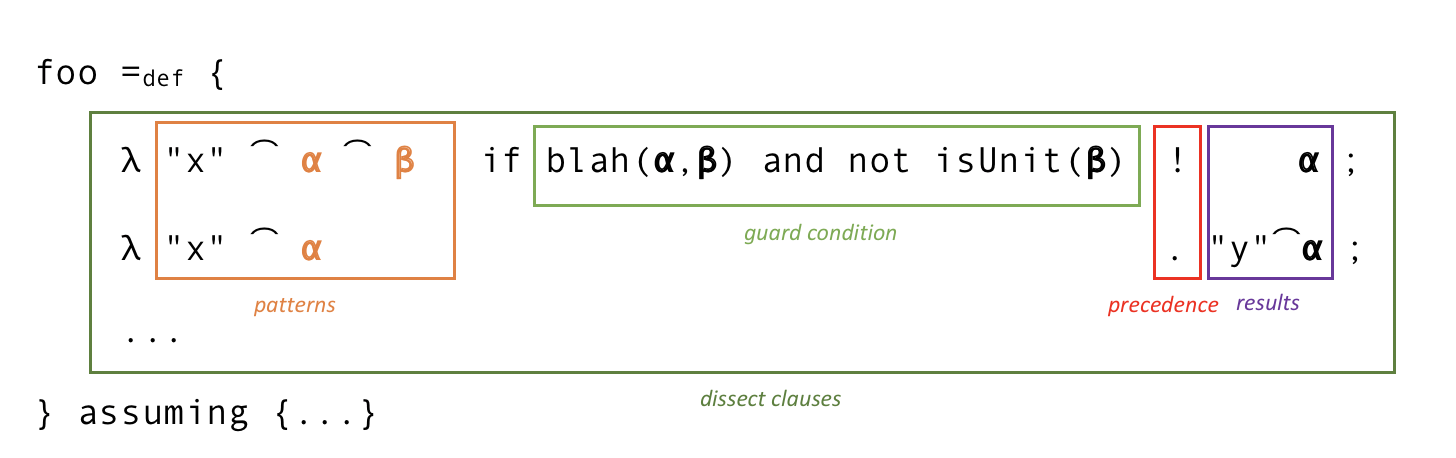
Let’s review some of the ways we’re talking about our piecemeal, recursive definitions expressed using dissect. Recall that something that looks like this:
foo =def {
...
}is always shorthand for:
foo (α) =def dissect α { ... }
Here is a diagram of a definition, with some of its parts labeled:

Remarks:
assuming {...} rule. (Often there are also some additional implicit assumptions, such as that some arguments will always be ∈ ℕ, others will always be strings over some alphabet Σ, and so on.)undefined. If on the other hand, a clause applies some function to an argument where no result is ever delivered (for example, because of a never-ending recursion), I’ll describe that as the result “being implicitly undefined.” When no clause applies to some legal argument, that’s also a case where the result is implicitly undefined.This table may help get clearer on the relationship between the categories of “being stinky” and “being winky”:

The fact that some arguments aren’t legal because they fail to satisfy an assuming {...} rule won’t by itself make a definition stinky. Neither will the fact that the definition explicitly declares the result for some legal argument to be undefined.
Here are ways that a definition does get to be stinky and not winky (the worst category):
Here is how a definition gets to be merely winky (but still stinky, the middling category):
Here are the examples I gave in our previous class (over Zoom):
foo =def {
λ α ⁀ β if α = "x" ! true;
λ α ⁀ β if β = "x" ! true;
γ . false
}That definition isn’t stinky. With arguments (“input values”) like "x" and "xax", multiple clauses with precedence ! will match, but they always deliver the same result.
bar =def {
λ "" ! true;
λ α ⁀ β if isUnit(α) . bar(β)
}That definition isn’t stinky. It will recurse in a specific predetermined way on ever-shrinking suffixes of its initial argument, until the first clause matches. In that definition, the result for any argument will eventually be true.
qux1 =def {
λ "" ! true;
λ α ⁀ β if isUnit(α) . undefined
}That definition isn’t stinky, because although it has no defined result for arguments that aren’t the empty string, it explicitly says so.
qux2 =def {
λ "" ! true;
λ α ⁀ β if isUnit(α) . qux2(α)
}This definition is stinky, because although it also has no defined result for arguments that aren’t the empty string, it doesn’t explicitly declare this. Instead it enters a never-ending recursion. (Contrast qux2, which will keep recursing on the same prefix α, to bar which recurses on the shrinking suffix β.)
Finally:
bez =def {
λ "" ! true;
λ α ⁀ β . bez(β)
}This is like bar, but we no longer require that α be non-empty. This definition is also stinky, but at the same time it at least manages to be winky. There’s always a way to dissect the function’s argument that will deliver a result (and always the same result). For example, if we apply bez to the argument "xy", that might recurse three times on the second clause, each time assigning α the value "" and β the value "xy". But then the next time through, it might assign α "x" and β "y". It might then recurse fifteen times assigning α the empty string again, and then finally assigning α "y" and β "". Whereupon the final recursive call will deliver the result true.
“Nondeterminism” is a label used in this literature to describe the kind of thing that happens in our dissect-definitions when more than one clause can match, or when a single clause can match against different ways of dissecting the input value.
Don’t let this label mislead you into thinking it has anything to do with chances or probabilities. In these contexts, it just means that there are multiple paths forward.
undefined); and this is understood to be the answer for the whole tree of available paths.bez) you can’t tell in advance which paths those will be.