Phil 455: Homework 7

This homework is due by the end of the day on Sun Mar 24.

Sample answers in purple.

Symbolize in first-order predicate logic with identity (=): (a) Andy loves Beverly, but she loves someone else. (b) Andy loves no one other than Beverly. Use this notation: a as a constant/name for Andy; b as a constant/name for Beverly; and L as a dyadic predicate (that is, a predicate taking two arguments), where Lxy means that x loves y.
1. Lab & ∃x(x ≠ a & Lbx). This doesn’t entail that Beverly fails to love Andy, which I’m assuming the English sentence doesn’t entail either (but only suggests or “implicates”). If you choose to interpret the English sentence differently, and formalize that different construal of it, that’s also ok, so long as your interpretation is reasonable and it’s clear what it is. Some example construals that entail Beverly fails to love Andy are: Lab & ∃x Lbx & ∀x(Lbx ⊃ x≠a) and Lab & ∃x Lbx & ¬Lba.
2. ∀x(Lax ⊃ x = b) or ¬∃x(Lax & x ≠ b). Neither of these entail that Andy loves Beverly, which I’m assuming the English sentence doesn’t entail either (but only suggests or “implicates”). As before, other reasonable interpretations of the English sentence can also be ok.
Symbolize this, using predicate logic with identity and “functors” (function symbols): If the father of a person is friends with each of the father’s co-workers, then that person’s mother has at least two sisters. Use this notation: C as a dyadic predicate, where Cxy or C(x,y) means that x and y are coworkers; F as a dyadic predicate, where Fxy means that x and y are friends; S as a dyadic predicate, where Sxy means that x and y are sisters; and f and m as monadic functors (that is, functors taking one argument), with f x and m x meaning the father and mother of x, respectively.

∀x(∀y(C(f x, y) ⊃ F(f x, y)) ⊃ ∃u∃v(u ≠ v & S(m x, u) & S(m x, v))).
Suppose we have a logical system with sentence constants like P, Q, and R, and logical operators like ⊃ and ¬. We also have variables φ and ψ in our metalanguage, that can stand in for arbitrary simple or complex sentences. Is (φ ⊃ ψ) ⊃ (¬φ ⊃ ¬ψ) a tautology, that is, something that logically has to be true, according to classical sentential logic? Explain your answer. (Hint: this question may be less straightforward than you first think.)

It depends on what sentences the metavariables φ and ψ stand for. For most sentences we’d substitute for them, no, not a tautology. But if φ and ψ are equivalent sentences (perhaps the same sentence), then yes. In fact it’s enough if ψ entails φ (including cases where φ is logically valid or ψ is logically false).
If φ stands for the formula Fx ⊃ ∀y(Gyx ∨ P ∨ ∃xHx), then: (a) What is φ[x ← w]? (b) What is φ[x ← y]? (c) What is φ[P ← ∀xGxy]? (Hint: variables that occur free in the terms being substituted in should still be free after the substitution.)
1. Fw ⊃ ∀y(Gyw ∨ P ∨ ∃xHx)
2. Fy ⊃ ∀y′(Gy′y ∨ P ∨ ∃xHx)
3. Fx ⊃ ∀y′(Gy′x ∨ ∀xGxy ∨ ∃xHx)
We’re going to do some syntactic manipulation of expresions in a logical language. First we’ll do it with the full resources of our dissect apparatus. This makes some things easy. In later problems we’ll work with a more restricted toolbox.

Our task here is to transform a formula φ into the result of replacing unbound occurrences of a variable ξ with a “closed term” τ. This is what I’m writing as φ[ξ ← τ]. (“Closed terms” are term constants like a and 1, and complex terms built up out of other closed terms. So no variables or complex terms that include variables. We confine our attention to closed terms here so that we don’t have to worry about renaming bound variables to avoid having free variables in τ being captured by quantifiers in the formula it’s being substituted into, as when we replace unbound occurences of x with y in ∃y(Qy ⊃ Rxy).)

To make things easier for ourselves here, we’ll assume that our language is sparse and regimented. The only logical connectives we’ll allow are ¬ and ⊃, and the quantifier ∀. We’ll be strict about requiring parentheses around any formula of the shape (ψ ⊃ φ). We’ll assume that complex terms always have the shape of a monadic functor η followed by one term, or the shape (β η α), where β and α are terms and η is a dyadic functor. We’ll assume that atomic formulas always have the shape of a monadic predicate ρ followed by one term, or the shape β ρ α, where β and α are terms and ρ is a dyadic predicate (including =). We don’t need to require parentheses here.

For the purposes of this problem, we’ll assume that no predicate, functor, term constant, or variable is a proper prefix or suffix of any other of these expressions. Thus if x and 1 are a variable and a term constant, we won’t also have variables like x1 or xx or x′, or predicates or functors like rx or f1.

We’ll help ourselves to functions isDyadicPredicate, isMonadicPredicate, isDyadicFunctor, isMonadicFunctor, isTermConstant, and isVariable that detect the corresponding expressions. These won’t be defined here.

The else at the end of the definitions below is just a pattern variable that matches any string that wasn’t matched by the earlier clauses. Before, I was making pattern variables for strings always be single Greek letters, but now we’ll start relaxing that convention.

Your job is to fill in the blanks.
```
isTerm(σ) =def dissect σ {
    λ "(" ⁀ β ⁀ η ⁀ α ⁀ ")" if isTerm(β) and isDyadicFunctor(η)! isTerm(α);
    λ η ⁀ α if isMonadicFunctor(η)! isTerm(α);
    λ else. isTermConstant(σ) or isVariable(σ)
}

isFormula(γ) =def dissect γ {
    λ "¬" ⁀ φ ! isFormula(φ);
    λ "(" ⁀ ψ ⁀ "⊃" ⁀ φ ⁀ ")" if isFormula(ψ)! ⸏⸏⸏a⸏⸏⸏;
    λ "∀" ⁀ ζ ⁀ φ if isVariable(ζ)! isFormula(φ);
    λ β ⁀ ρ ⁀ α if isTerm(β) and isDyadicPredicate(ρ)! isTerm(α);
    λ ρ ⁀ α if isMonadicPredicate(ρ)! ⸏⸏⸏b⸏⸏⸏;
    λ else. false
}

replaceUnbound(γ, ξ, τ) =def dissect γ {
    λ "¬" ⁀ φ ! "¬" ⁀ replaceUnbound(⸏⸏⸏c⸏⸏⸏, ξ, τ);
    λ "(" ⁀ ψ ⁀ "⊃" ⁀ φ ⁀ ")" if isFormula(ψ)! ⸏⸏⸏d⸏⸏⸏;
    λ "∀" ⁀ ζ ⁀ φ if isVariable(ζ) and ζ ≠ ξ! "∀" ⁀ ζ ⁀ replaceUnbound(⸏⸏⸏e⸏⸏⸏, ξ, τ);
    λ β ⁀ ρ ⁀ α if isTerm(β) and isDyadicPredicate(ρ)! replaceInTerm(β, ξ, τ) ⁀ ρ ⁀ replaceInTerm(α, ξ, τ);
    λ ρ ⁀ α if isMonadicPredicate(ρ)! ρ ⁀ replaceInTerm(α, ξ, τ);
    λ else. γ
} assuming { λ γ if isFormula(γ) }

replaceInTerm(σ, ξ, τ) =def dissect σ {
    λ "(" ⁀ β ⁀ η ⁀ α ⁀ ")" if isTerm(β) and isDyadicFunctor(η)! "(" ⁀ replaceInTerm(β, ξ, τ) ⁀ η ⁀ replaceInTerm(α, ξ, τ) ⁀ ")";
    λ η ⁀ α if isMonadicFunctor(η)! η ⁀ replaceInTerm(α, ξ, τ);
    λ α if isVariable(α) and α = ξ! ⸏⸏⸏f⸏⸏⸏;
    λ else. ⸏⸏⸏g⸏⸏⸏
} assuming { λ σ if isTerm(σ) }
```
1. isFormula(φ)
2. isTerm(α)
3. φ
4. "(" ⁀ replaceUnbound(ψ, ξ, τ) ⁀ "⊃" ⁀ replaceUnbound(φ, ξ, τ) ⁀ ")"
5. φ
6. τ
7. σ
Now we’re going to do syntactic tests and manipulation by a different strategy. Rather than having parentheses, we’ll suppose that our language instead uses a form of Polish Notation. This comes in several forms. We’ll use the form that’s read from right to left. Here are examples of some formulas written in the traditional style, and beside them how they’d be written in our Polish Notation:

Traditional Polish

¬(P ⊃ Q) Q P ⊃ ¬

(¬P) ⊃ Q Q P ¬ ⊃

P ⊃ ¬ Q Q ¬ P ⊃

Here’s another example to help you understand this notation. Consider the formula (Bx ⊑ x) ⊃ (¬ Hx). Here’s a parse tree for that formula. I’ve placed all predicates, functors, and operators to the left, even if (as with ⊑ and ⊃) they’re traditionally written in the middle.

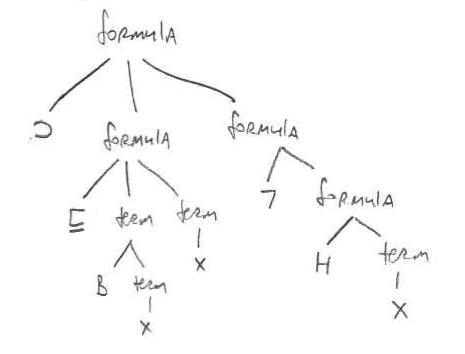
Now read the fringe of this tree from right to left. That gives us: x H ¬ x x B ⊑ ⊃, which is the Polish Notation for this formula.

Let’s work with a specific language, designed to express claims about strings. We’ll let our variables be x, x′, x″, and so on. We’ll have one term constant ε and two monadic term functors A and B. The meaning of Ax will be what we’d before express as "a" ⁀ x, but in this language we don’t have term constants like "a". Similarly the meaning of Bx will be what we’d before express as "b" ⁀ x. We’ll still have the dyadic term functor ⁀, so that we can build complex terms like (the Polish versions of) x ⁀ x′ and (Bx′) ⁀ x. We’ll have the dyadic predicates = and ⊑, where (the Polish version of) x ⊑ x′ means that x is a prefix of x′. And the monadic predicate H, where Hx means that x is either ε or Aε (what we’d earlier write as "a") or Bε (what we’d earlier write as "b"). (We can call this the claim that x is short.) We also have the logical symbols ⊃, ¬, and ∀.
1. Consider this formula of the language just described: ∀x(Hx ⊃ ∀x″(¬(x ⊑ Bx″) ⊃ (x ⊑ Aε))). Given the intended meaning for these symbols, is it possible, necessary, or neither for the formula to be true?
  
  Note that claims of the form ¬φ ⊃ ψ “say roughly” that either φ or ψ is true. (This is how you express disjunction in a language whose logical operators include only ⊃ and ¬.) Given that, the formula here says roughly that every short string x is either a prefix of every string x″ beginning with "b" or is a prefix of the string "a". That has to be true.
2. Write that formula in our Polish Notation. We’ll write a variable like x″ as x ′ ′, with the syntax treating each prime as if it were a monadic functor. (Semantically, though, ′ won’t be a functor; the whole expression x ′ ′ is instead a single variable, which is a kind of atomic term.)
  
  ε A x ⊑ x ′ ′ B x ⊑ ¬ ⊃ x ′ ′ ∀ x H ⊃ x ∀
3. Here is a formula written in our Polish Notation: x ′ B x ⁀ x ⊑ x ∀ x ′ ∀. Write that formula in traditional form.
  
  ∀x′ ∀x (x ⊑ (x ⁀ Bx′))
4. Given the intended meaning for these symbols, is it possible, necessary, or neither for the formula to be true?
  
  This says roughly that every pair of strings x′, x are such that x is prefix of x ⁀ "b" ⁀ x′. This has to be true.

Traditional	Polish
`¬(P ⊃ Q)`	`Q P ⊃ ¬`
`(¬P) ⊃ Q`	`Q P ¬ ⊃`
`P ⊃ ¬ Q`	`Q ¬ P ⊃`

Polish Notation may seem like a pain and be hard to read, but it makes what we’ll do next much easier. We’re going to make use of two auxiliary functions, defined like this:

lastUnit =def {
    λ α ⁀ β if isUnit(β)! β;
    λ "". undefined
}

allButLast =def {
    λ α ⁀ β if isUnit(β)! α;
    λ "". undefined
}

What we’re aiming for is to define a function takeVar that should map a Polish Notation string ending in a variable (… x or … x ′ ′ or so on) and return just the variable part (after the …); and a function dropVar that should return just the … part. Similarly for takeTerm/dropTerm and takeFormula/dropFormula.

Your job is to fill in the blanks.

If one of the functions returns an undefined result, and that is supplied as an argument to another function, the result is understood to always also be undefined.

takeVar(σ) =def dissect lastUnit(σ) {
    λ "x". "x";
    λ "′". takeVar(allButLast(σ)) ⁀ "′";
    λ else. undefined
}

dropVar(σ) =def dissect lastUnit(σ) {
    λ "x". allButLast(σ);
    λ "′". dropVar(allButLast(σ));
    λ else. undefined
}

takeTerm(σ) =def dissect lastUnit(σ) {
    λ "B". takeTerm(allButLast(σ)) ⁀ "B";
    λ "A". takeTerm(allButLast(σ)) ⁀ "A";
    λ "ε". "ε";
    λ "⁀". takeTerm(dropTerm(allButLast(σ))) ⁀ ⸏⸏⸏a⸏⸏⸏ ⁀ "⁀";
    λ else. takeVar(σ)
}

dropTerm(σ) =def dissect lastUnit(σ) {
    λ "B". dropTerm(allButLast(σ));
    λ "A". dropTerm(allButLast(σ));
    λ "ε". allButLast(σ);
    λ "⁀". ⸏⸏⸏b⸏⸏⸏ ;
    λ else. dropVar(σ)
}

takeFormula(γ) =def dissect lastUnit(γ) {
    λ "=". takeTerm(dropTerm(allButLast(γ))) ⁀ ⸏⸏⸏c⸏⸏⸏ ⁀ "=";
    λ "⊑". ⸏⸏⸏d⸏⸏⸏ ⁀ takeTerm(allButLast(γ)) ⁀ "⊑";
    λ "H". takeTerm(allButLast(γ)) ⁀ "H";
    λ "¬". takeFormula(allButLast(γ)) ⁀ "¬";
    λ "⊃". ⸏⸏⸏e⸏⸏⸏ ⁀ takeFormula(allButLast(γ)) ⁀ "⊃";
    λ "∀". takeFormula(dropVar(allButLast(γ))) ⁀ takeVar(allButLast(γ)) ⁀ "∀";
    λ else. undefined
}

dropFormula(γ) =def dissect lastUnit(γ) {
    λ "=". dropTerm(dropTerm(allButLast(γ)));
    λ "⊑". dropTerm(dropTerm(allButLast(γ)));
    λ "H". ⸏⸏⸏f⸏⸏⸏ ;
    λ "¬". dropFormula(allButLast(γ));
    λ "⊃". dropFormula(dropFormula(allButLast(γ)));
    λ "∀". ⸏⸏⸏g⸏⸏⸏ ;
    λ else. undefined
}

Once you’ve figured these definitions out, you should be equipped to define notions like take1stSubFormula (which when applied to a string ending with ψ ⁀ φ ⁀ "⊃" would return φ) and replaceUnbound (from Problem 81, above, this will also require redefining replaceInTerm). I won’t assign these as part of this Homework, but you’re welcome to do them as extra credit.

takeTerm(allButLast(σ))
dropTerm(dropTerm(allButLast(σ)))
takeTerm(allButLast(γ))
takeTerm(dropTerm(allButLast(γ)))
takeFormula(dropFormula(allButLast(γ)))
dropTerm(allButLast(γ))
dropFormula(dropVar(allButLast(γ)))

Here are the extra credits. As in Problem 81, we assume that τ is a closed term, so that we don’t have to worry about renaming bound variables to avoid having free variables in τ being captured by quantifiers in the formula it’s being substituted into.

take1stSubFormula(γ) =def dissect lastUnit(γ) {
    λ "¬". takeFormula(allButLast(γ));
    λ "⊃". takeFormula(allButLast(γ));
    λ "∀". takeFormula(dropVar(allButLast(γ)));
    λ else. undefined
}

replaceUnbound(γ, ξ, τ) =def dissect lastUnit(γ) {
    λ "=". replaceInTerm(takeTerm(dropTerm(allButLast(γ))), ξ, τ) ⁀ replaceInTerm(takeTerm(allButLast(γ)), ξ, τ) ⁀ "=";
    λ "⊑". replaceInTerm(takeTerm(dropTerm(allButLast(γ))), ξ, τ) ⁀ replaceInTerm(takeTerm(allButLast(γ)), ξ, τ) ⁀ "⊑";
    λ "H". replaceInTerm(takeTerm(allButLast(γ)), ξ, τ) ⁀ "H";
    λ "¬". replaceUnbound(takeFormula(allButLast(γ)), ξ, τ) ⁀ "¬";
    λ "⊃". replaceUnbound(takeFormula(dropFormula(allButLast(γ))), ξ, τ) ⁀ replaceUnbound(takeFormula(allButLast(γ)), ξ, τ) ⁀ "⊃";
    λ "∀" if takeVar(allButLast(γ)) ≠ ξ ! replaceUnbound(takeFormula(dropVar(allButLast(γ))), ξ, τ) ⁀ takeVar(allButLast(γ)) ⁀ "∀";
    λ "∀". γ;
    λ else. undefined
}

replaceInTerm(σ, ξ, τ) =def dissect lastUnit(σ) {
    λ "B". replaceInTerm(takeTerm(allButLast(σ)), ξ, τ) ⁀ "B";
    λ "A". replaceInTerm(takeTerm(allButLast(σ)), ξ, τ) ⁀ "A";
    λ "ε". "ε";
    λ "⁀". replaceInTerm(takeTerm(dropTerm(allButLast(σ))), ξ, τ) ⁀ replaceInTerm(takeTerm(allButLast(σ)), ξ, τ) ⁀ "⁀";
    λ else if takeVar(σ) = ξ ! τ;
    λ else. takeVar(σ)
}

Our final exercise with syntactic manipulation will treat our Polish Notation expressions of the language described in Problem 82 as base 12 numerals. We’ll write base 12 (or “duodecimal”) numerals with a 0d prefix, and the digits after 9 will be a and b. Unlike Problem 76 in the previous homework, these numerals will be read in the usual left-to-right order. Thus, here is an ascending sequence of base 12 numerals: 0d9, 0da, 0db, 0d10, 0d11, 0d12. The last numeral represents 1⋅twelve + 2⋅one or fourteen. The base 12 numeral 0d123 represents 1⋅one hundred forty-four + 2⋅twelve + 3⋅one or one hundred seventy-one.

We’ll translate our Polish notation strings into base 12 numerals unit by unit, using the following correspondences:

String Unit Numeral

B 0db

A 0da

ε 0d9

x 0d8

′ 0d7

⁀ 0d6

= 0d5

⊑ 0d4

H 0d3

¬ 0d2

⊃ 0d1

∀ 0d0

Thus here is the translation of the Polish Notation formula given in Problem 82c:

x ′ B x ⁀ x ⊑ x ∀ x ′ ∀ 0d 8 7 b 8 6 8 4 8 0 8 7 0

It’s important in this scheme that the symbol mapped to digit 0 would never occur at the left-hand side of a well-formed expression of our Polish Notation language. Why?

Your task is to translate the six main definitions from Problem 83 into arithmetical form, operating on numbers rather than string. You can help yourself to the following auxiliary functions:
- ordinary addition
- len(n) is the number of base 12 digits it takes to represent the number n, with len(n) being one for zero ≤ n < twelve, being two for twelve ≤ n < one hundred forty-four, and so on.
- n mod12 gives the remainder when the number n is divided by twelve. Thus 0d123 mod12 is 0d3.
- n >> k divides the number n by twelve to the kth power, discarding any remainder. Thus 0d123 >> 0d2 is 0d1.
- n << k multiplies the number n by twelve to the kth power. Thus 0d1 << 0d2 is 0d100.
Here is how to translate the first three functions:
```
takeVar(n) =def dissect n mod12 {
    λ 0d8. 0d8;
    λ 0d7. takeVar(n >> 0d1) << 0d1 + 0d7;
    λ else. undefined
}

dropVar(n) =def dissect n mod12 {
    λ 0d8. n >> 0d1;
    λ 0d7. dropVar(n >> 0d1);
    λ else. undefined
}

takeTerm(n) =def dissect n mod12 {
    λ 0db. takeTerm(n >> 0d1) << 0d1 + 0db;
    λ 0da. takeTerm(n >> 0d1) << 0d1 + 0da;
    λ 0d9. 0d9;
    λ 0d6. takeTerm(dropTerm(n >> 0d1)) << (0d1 + len(takeTerm(n >> 0d1))) + takeTerm(n >> 0d1) << 0d1 + 0d6;
    λ else. takeVar(n)
}
```
Now you translate the last three.
```
dropTerm(n) =def dissect n mod12 {
    λ 0db. dropTerm(n >> 0d1);
    λ 0da. dropTerm(n >> 0d1);
    λ 0d9. n >> 0d1;
    λ 0d6. dropTerm(dropTerm(n >> 0d1));
    λ else. dropVar(n)
}

takeFormula(n) =def dissect n mod12 {
    λ 0d5. takeTerm(dropTerm(n >> 0d1)) << (0d1 + len(takeTerm(n >> 0d1))) + takeTerm(n >> 0d1) << 0d1 + 0d5;
    λ 0d4. takeTerm(dropTerm(n >> 0d1)) << (0d1 + len(takeTerm(n >> 0d1))) + takeTerm(n >> 0d1) << 0d1 + 0d4;
    λ 0d3. takeTerm(n >> 0d1) << 0d1 + 0d3;
    λ 0d2. takeFormula(n >> 0d1) << 0d1 + 0d2;
    λ 0d1. takeFormula(dropFormula(n >> 0d1)) << (0d1 + len(takeFormula(n >> 0d1))) + takeFormula(n >> 0d1) << 0d1 + 0d1;
    λ 0d0. takeFormula(dropVar(n >> 0d1)) << (0d1 + len(takeVar(n >> 0d1))) + takeVar(n >> 0d1) << 0d1 + 0d0;
    λ else. undefined
}

dropFormula(n) =def dissect n mod12 {
    λ 0d5. dropTerm(dropTerm(n >> 0d1));
    λ 0d4. dropTerm(dropTerm(n >> 0d1));
    λ 0d3. dropTerm(n >> 0d1);
    λ 0d2. dropFormula(n >> 0d1);
    λ 0d1. dropFormula(dropFormula(n >> 0d1));
    λ 0d0. dropFormula(dropVar(n >> 0d1));
    λ else. undefined
}
```

String Unit	Numeral
`B`	0db
`A`	0da
`ε`	0d9
`x`	0d8
`′`	0d7
`⁀`	0d6
`=`	0d5
`⊑`	0d4
`H`	0d3
`¬`	0d2
`⊃`	0d1
`∀`	0d0