Phil 455: Homework 3

This homework is due by the end of the day on Fri, Feb 9.

Sample answers in purple.

What’s a more familiar name for a symmetric preorder?

This would be an equivalence relation: transitive, reflexive, and symmetric. An unintuitive limiting case of an “order.”
Is the relation “is a prefix (initial substring) of” on the set of strings over an alphabet well-founded? Does it constitute a total order?

Yes, that relation is well-founded. It might not be total. If the alphabet has only a single letter, the relation will be total, but if it has more letter it won’t be. Distinct strings can be such that neither is a prefix of the other.
Examples 2 and 3 on the order webnotes were:

Example 2

0 ⊏ 2 ⊏ 4 ⊏ ... ⊏ 1 ⊏ 3 ⊏ 5 ⊏ ...

Example 3

0 ⊏ 2 ⊏ 3 ⊏ 4 ⊏ 5 ⊏ ... ⊏ 1

These are just suggestive representations of the two orderings. Specify them each more rigorously, by saying something of the form “the graph of the first relation is {(x,y) ∈ ℕ² | blah-blah}.”

Example 1’s strict order has the graph {(x,y) | ((x and y are both even or both odd) & x < y) ∨ (x is even and y is odd)}.

Example 3’s strict order has the graph {(x,y) | x ≠ 1 & (x < y ∨ y = 1)}.
Consider the order relation on elements of ℕ² whose graph is {((x,y),(x′,y′)) | x ≤ x′ and y ≤ y′}, where ≤ is the familiar less-than relation on ℕ. Is this order relation weakly connected? Is it well-founded? Justify your answers.

It’s not weakly connected: for example, (0,1) is incomparable with (1, 0).

It is well-founded. Take any non-empty set of (x,y) in the relation’s domain. Let x_min be the x component that is least (by ≤) among this set. Let y_min be the y component that is least among the pairs whose first component is x_min. Then no element in the set will be less than (x_min, y_min), though some may be incomparable.
In Example 12 of the order webnotes, we considered the set of all strings formed from the letters "a" and "b", ordered by the relation of being a substring of. We said that that ordering was well-founded, but not total. Consider the following, alternative ordering of these strings, which is total:

string xs ⊏ string ys =def string ys is non-empty, and either: a. xs is a prefix of ys; or b. there are (possibly empty) strings us, vs, and ws such that: xs = us ⁀ "a" ⁀ vs (that is, xs is the result of concatenating string us to the letter "a" and that to the string vs) and ys = us ⁀ "b" ⁀ ws.

According to this ordering: "a" ⊏ "aa" ⊏ "aab" ⊏ "ab" ⊏ "b".

This is called the lexicographic ordering of the strings, as it’s based on the way dictionaries order words. Prove that this ordering is not well-founded.

(Hint: try to add more elements into the example ordering between aa and aab.)

There are infinitely descending chains, like in Examples 8 and 9 of the order webnotes. For example: ... ⊏ "aaaab" ⊏ "aaab" ⊏ "aab" ⊏ "ab" ⊏ "b".
Return to the mod function from Homework 2 Problem 32. Let Β be the set {2,3,5,6,10,15,30} and let R be the relation on Β whose graph is {(y,x) | x mod y = 0}.
1. List the elements of R and show that it is a non-strict partial order but not a total order.
2. Identify any maximal, minimal, greatest, and/or least elements in this order.
3. Do the same as (a) and (b) but for the set 𝟚^Γ, where Γ is {"a","b","c"}, and the relation is ⊆. (Recall that 𝟚^Γ means “the powerset of Γ.”)
1. R’s graph is {(2,2),(3,3),(5,5),(6,6),(10,10),(15,15),(30,30),(2,6),(2,10),(2,30),(3,6),(3,15),(3,30),(5,10),(5,15),(5,30),(6,30),(10,30),(15,30)}. It’s clearly reflexive and can by inspection be verified to be anti-symmetric and transitive, so it’s a non-strict partial order. Many pairs of elements (for example, any two of 2, 3, 5) are incomparable, so it’s not a total order.
2. 30 is greatest (and so maximal); 2 and 3 and 5 are minimal.
3. 𝟚^{{"a","b","c"}} has the same structure as R, except that it adds a least element ∅. The greatest element in this case is {"a","b","c"} itself.
For any set Β, consider the partial ordering of 𝟚^Β by ⊆. (a) Will any two elements Γ, Δ of that domain have a least upper bound or “join,” and if so, what is it? (b) Will they have a greatest lower bound or “meet,” and if so, what is it? (c) Does this partial ordering count as a lattice? If so, say whether it has a top and/or bottom element.
1. Yes, their join is Γ ∪ Δ.
2. Yes, their meet is Γ ∩ Δ.
3. Yes, it’s a bounded lattice, with top being Β and bottom being ∅.
Consider the following diagrams of posets (with a ⊏ b being represented by a being below b and connected by an always-upwards path). Which of these posets are lattices?

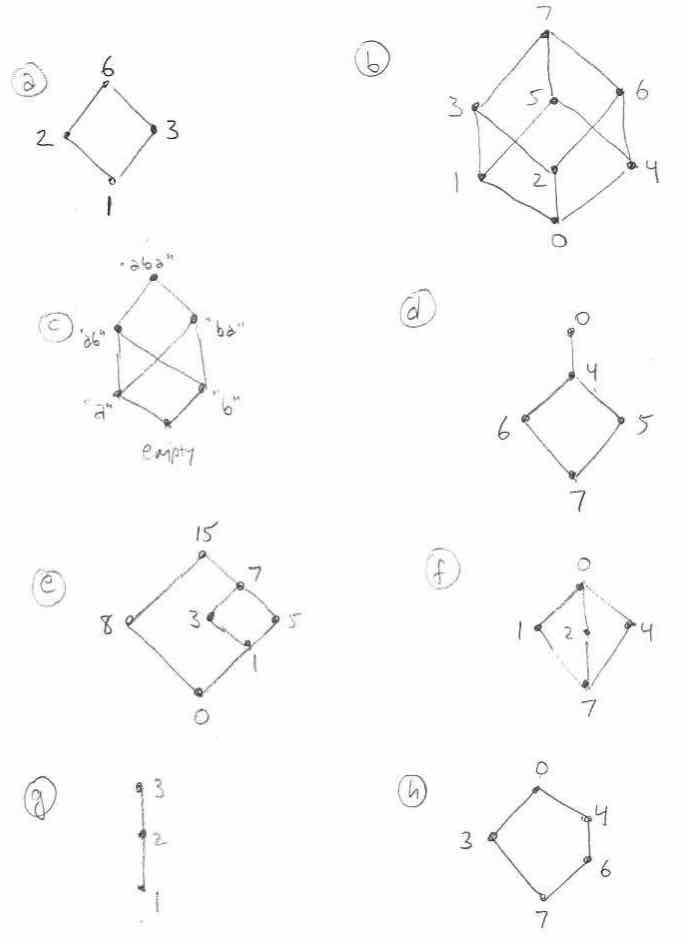
All of the diagrams except (c) are lattices.

(c) fails to be a lattice because although a and b have three upper bounds, none of them is least.
Consider the following acyclic ugraph with just one component:

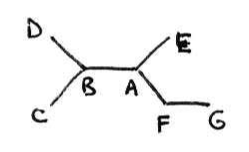
If we designate some node as the root and impose a “precedence” order on the nodes of this graph, to turn it into a tree, which of the following sequences are ones we might end up with as fringes of the tree? Defend your answers.
1. D, C, E Yes, if the root is G and the precedence order has D < B < C < A < E
2. D, C, G, E Yes, if the root is A and the precedence order has D < B < C < F < E. G could either come just before or just after F.
3. E, C, D, G Yes, if the root is A and the precedence order has E < D < B < C < F. Again, G could either come just before or just after F.
4. G, D, E, C This could not be a fringe. For these four to be the leaves, the root would have to be A. But then if B < E in the precedence order, C would have to precede E in the fringe. If on the other hand E < B in the precedence order, E would have to precede D in the fringe. Since neither holds, this sequence could not be a fringe of a tree built from this graph.
Let 𝔽 be the set of finite subsets of ℕ. Prove that 𝔽 is countably infinite, that is, that |𝔽| = |ℕ|.

We specify a bijection between each S ∈ 𝔽 and the sum for all n ∈ S of 2ⁿ.
Let 𝕀 be the set of infinite subsets of ℕ (that is, 𝕀 = 𝟚^ℕ – 𝔽). 𝕀 itself is uncountable (whenever you take away a countable set like 𝔽 from an uncountable set like 𝟚^ℕ, the result will still be uncountable). But specify a countably infinite subset of 𝕀, and justify your claim that it is countably infinite.

One easy example is the set {ℕ - {x} | x ∈ ℕ}. There’s an obvious bijection between the sets that are members of this set, and the natural numbers (each set is paired with the single natural number it omits). So there are countably many of these sets, and each of these sets is itself countably infinite, so is a member of 𝕀 not of 𝔽.

Here’s another example. Let 𝔾 be the set of all subsets of ℕ that omit only finitely many elements of ℕ (these are called “cofinite subsets of ℕ,” and each will be a member of 𝕀). We map each S ∈ 𝔾 to ℕ – S, which will be a member of 𝔽. This will be a bijection from 𝔾 to 𝔽, so these sets will have the same cardinality. We proved in Problem 43 that 𝔽 has the same cardinality as ℕ.