Relations can hold between elements of different domains. For example, there’s the binary relation between students and grades that holds iff the student ever was given that grade for a class. When a binary relation holds between elements of the same domain Α, the relation is called homogeneous (not “homogenous”), or just described as “a relation on Α” or “a relation over Α.”
Here again are some vocabulary describing special categories of some binary relations:
A binary relation
Ris reflexive iff it holds between all of its arguments and themselves. This is just a rough statement of the idea. To refine it, we have to consider cases like these: say, relations that hold between every male parent and himself, and may also hold between him and his children, but don’t hold between any female parents and anything / anyone else. Should we count this relation as reflexive? We might say it’s reflexive on the domain of male parents, but not reflexive on the domain of parents in general. Or we might count a relation as reflexive iff whenever it holds betweenxand anything, it also holds betweenxandx. But it’s permitted not to hold between some members of its domain and anything else. (This would be a “partial relation,” akin to the notion of a “partial functon”.) If we said the latter, then the relation could be “reflexive” on the domain of parents in general. Both of these notions are interesting. Standard terminology, though, uses “reflexive” only in the former way. That is, every member of the domain has to stand in the relation to itself.When a relation fails to be reflexive, say that it’s “not reflexive.” There’s also a technical notion of a relation’s being irreflexive. This means that the relation never holds between
xandx.A binary relation
Ris symmetric iff whenever it holds betweenxandy, it also holds betweenyandx.When a relation fails to be symmetric, say that it’s “not symmetric.” There are also technical notions of a relation’s being asymmetric and its being anti-symmetric, which we’ll explain below. They are not the same as the relation’s failing to be symmetric. I don’t think all of this vocabulary is very well-chosen. But unfortunately it is very well-entrenched.
A binary relation
Ris transitive iff whenver it holds betweenxandyand betweenyandz, then it also holds betweenxandz.When a relation fails to be transitive, say that it’s “not transitive.” There’s also a technical notion of a relation’s being intransitive or anti-transitive. Different authors use different terminology. This means that whenever there are
x,y, andzsuch that the relation holds betweenxandyand also betweenyandz, it never holds betweenxandz(that is, for nox,y, andzdoes that obtain, even when some of these are identical). Partee gives the example of theis the mother ofrelation among human beings.Observe that
⊆is a transitive relation, and that∈is not a transitive relation, but neither is it intransitive. (LetΒbe{Α}andΓbe{{Α}, Α}. ThenΑ ∈ ΒandΒ ∈ Γ, but alsoΑ ∈ Γ.)
Now we expand on that list. As before, we’re considering only binary relations between a domain and itself:
The identity relation on a domain holds between every element of the domain and itself, and between no other arguments. (So this relation is reflexive, though usually there will be other relations that are reflexive too.)
The universal relation on a domain holds between every pair of elements in the domain (including pairs where it’s the same element taken twice).
A relation is asymmetric iff whenever it holds between x and y, it won’t hold between y and x. (This entails that the relation is irreflexive.)
A relation is anti-symmetric iff whenever it holds between x and y for distinct x and y, it won’t hold between y and x. In other words: xRy & yRx implies x = y. This category doesn’t constrain whether elements do or don’t have the relation to themselves.
Asymmetry implies anti-symmetry, but observe that anti-symmetry doesn’t imply asymmetry. It doesn’t even imply a lack of symmetry: for example, the identity relation on a domain can be both symmetrical and anti-symmetrical. Note that none of these symmetry properties require that the relation does hold in one direction or the other between a given x and y. We’ll discuss requirements like that later.
Anti-symmetry plus irreflexivity does imply (is equivalent to) asymmetry.
Some relations are neither symmetrical, nor anti-symmetrical, nor asymmetrical: for example, the relation on {1,2,3} whose graph is {(1,2),(2,1),(1,3)}.
Similarly, some relations are neither reflexive nor irreflexive: for example, the relation on {1,2} whose graph is {(1,1),(2,1)}.
When we talked about functions, we distinguished between “partial” and “total” functions on a domain. (When the qualifier is omitted, in this case it’s assumed to be “total.” We’ll see other cases where an omitted “partial” or “total” is assumed to be “partial.”) The idea here is, does the function give a value for every element of its domain?
When we think about a relation being “total” or “complete” on its domain, there’s a bunch of different properties that could claim to capture at least part of that idea. In this list, the quantifiers are all understood as ranging over R’s domain.
R is serial or left-total: ∀x ∃y (xRy)∀x ∀y (x ≠ y ⊃ (xRy ∨ yRx))∀x ∀y (xRy ∨ yRx) — this is equivalent to the combination of property (b) plus reflexivity∀x ∀y (exactly one of these three hold: x = y, xRy, yRx) — this is equivalent to the combination of property (b) plus asymmetry∀x ∀y (xRy) — then R is the universal relation on its domainThe terms complete and total for relations, and also the term connected, don’t have uniform usages. Various authors use them for different items from this list (or for yet other notions).
Note that property (b) doesn’t constrain whether elements of the domain have the relation to themselves. Maybe they always do; maybe they never do; maybe some do and some don’t. Sometimes (b) is called “weakly connected” and (c) is called “strongly connected”; I’ll use that vocabulary. Two of our readings for this week (Partee and the Open Logic Project) use “connected” to mean (b)/weakly connected.
Note that “connectedness” means something else for a graph structure.
When for a specific choice of x, y, at least one of xRy or yRx holds, we say that x and y are comparable by that relation. So another way to express property (b) is to say that all pairs of distinct objects from the domain are comparable.
Here are some further properties also capturing a kind of completeness for relations:
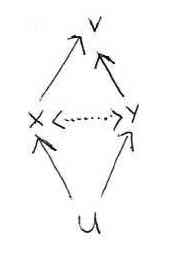
∀u ∀x ∀y ((uRx & uRy) ⊃ x and y have R to each other) ∀v ∀x ∀y ((xRv & yRv) ⊃ x and y have R to each other) These are called Euclidean properties. This illustration may help:

Property (f) says that whenever the two relations at the bottom hold (from u to x and to y), then x and y have the relation to each other (the dotted arrows in the middle). Property (g) says that whenever the two relations at the top hold (from x and from y to v), then in that case x and y have the relation to each other. For symmetric relations, transitivity coincides with property (f) and with property (g); but in general being transitive and being Euclidean aren’t the same.
A relation is called an equivalence relation iff it’s reflexive, symmetric, and transitive. The identity relation for a domain is an equivalence relation, but usually there will be other equivalence relations too. Authors often use the symbols ≡ or ≈ or ~ to represent an equivalence relation.
As the readings explain, there is a close connection between equivalence relations and partitions of a set, which were defined as: divisions of the set into one or more (non-empty) “cells,” where everything from the original set gets to be in one of the cells, and none of the cells overlap.
Given a partition P of a set Α, there is an equivalence relation defined as “belong to the same cell of P.”
Given an equivalence relation R on domain Α, there is a partition of Α where elements belong to the same cell iff R holds between them. For a specific a ∈ Α, its cell in this partition is sometimes written as [a]R, other times as ⟦a⟧R. When R is clear from context, the subscript is sometimes omitted — though each of the notations [a] and ⟦a⟧ are also used in other ways in the material we’re considering this term. (This sort of thing happens all the time. I regret it, but that’s how it is.)
In all cases the domain is assumed to be only humans:
 Earlier I had written this was anti-symmetric, but that’s wrong, as distinct people can be at least as tall as each other.)
Earlier I had written this was anti-symmetric, but that’s wrong, as distinct people can be at least as tall as each other.)In class, we talked about the notion of a set Α being closed under a relation R. We assume R is a binary relation on a domain Δ (which is a superset of Α). Then this means: ∀a ∈ Α ∀x ∈ Δ (Rax ⊃ x ∈ Α).
(Generalizing, if R is an ternary relation on Δ, Α is closed under R iff ∀a ∈ Α ∀b ∈ Α ∀x ∈ Δ (Rabx ⊃ x ∈ Α). And so on.)
We talked also about the closure of a set Α under such a relation. This means the “smallest” superset of Α that is closed under the relation. (Here understanding one set to be smaller than the other when it’s a proper subset. We’ll discuss other ways of comparing the sizes of sets in later classes.) Equivalently, you could define this as the intersection of all supersets of Α that are closed under the relation.
Theorists also talk about closures of relations. For example, the reflexive closure of a relation R is the relation whose graph is {(x,y) | xRy ∨ x = y}. If R is already reflexive, this will be the same relation.
The symmetric closure of a relation R is the relation whose graph is {(x,y) | xRy ∨ yRx}. If R is already symmetric, this will be the same relation.
The transitive closure of a relation is a bit more complicated to define rigorously, but the intuitive idea is like what we’ve just done. Recall that x stands in the composition of relation R₁ and relation R₂ to z (written (R₂ ∘ R₁)xz) iff there’s some y such that x stands in R₁ to y and y stands in R₂ to z. Recall also we had the notation with functions that f¹ = f, f² = f ∘ f, f³ = f ∘ f ∘ f, and so on. Similarly, we can define R¹ = R, R² = R ∘ R, R³ = R ∘ R ∘ R. In general, Rk+1 = R ∘ Rk = Rk ∘ R.
Then the transitive closure of R (sometimes written as R+) can be defined as the relation whose graph is the union of all the Rks for k > 0. That is, 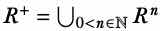 .
.
Here’s another way to think about the transitive closure of a relation R on domain Α. Define a new relation ρ on pairs of As such that (a,b)ρ(a′,c) iff a = a′ & bRc. Above we explained the notion of a closure of a set under a relation. Consider the graph of R (which will be a subset of Α²) and take its closure under relation ρ. Call this resulting set Ρ. Then whenever aRb & bRc, (a,b) will be ∈ R’s graph (and so also ∈ its superset Ρ) and will bear ρ to (a,c) (by the definition of ρ), thus since Ρ is closed under ρ, (a,c) will be ∈ Ρ. The relation whose graph is Ρ will be the transitive closure of R.
Often theorists want to work with what’s both the transitive and reflexive closure of a relation. This is the relation whose graph is the union of the graphs of:
R’s domain (which can be written as R⁰)The transitive and reflexive closure of R is sometimes written as R*. The general idea behind these superscripts is that * means “0 or more times” and + means “1 or more times.” (Other times R* is used to mean what I’m writing as R+.)
Examples:
If R is the relation “is a parent of,” then R+ would be the relation “is an ancestor of”. (Indeed, another way of describing the transitive closure of R is as “the ancestral of R.”) R* would be the relation which is like R+, but which people also stand in to themselves.
Let S be the successor relation on ℕ: that is, let xSy mean that y is a successor of x. So 0S1, 1S2, 2S3, and so on. But it’s not the case that 0S2, 0S3, and so on. However 0 will stand in S+ to 2 and to 3. Indeed S+ is equivalent to the relation < on ℕ. And S* is equivalent to the relation ≤.
Back in our review of sets, I wrote:
I talked about the “first” and “second” element of an ordered pair. But the suggestion of an “order” to these elements can mislead. Really the important thing is just that we keep track of which element comes from which set, or which element comes from a single set playing the role of one side of the Cartesian product rather than the other. Instead of the “first” element and the “second” element, we could instead talk about the “west” element and the “east” element. And for ordered quadruples, about the “north,” “south,” “east” and “west” elements. If someone then took it in mind to ask whether the west element comes before or after the east element, this question wouldn’t have any established sense.
Similarly, if you take the ordered quadruple
(a,b,c,d), we might call it “increasing” iffa ≤ b ≤ c ≤ d. But I could just as easily define another notion, call it “ascending,” which holds iffa ≤ d ≤ b ≤ c. There’s no sense in which one of these two notion is more intrinsically natural or less gruesome than the other.
With strings, on the other hand, the collection does have a more natural intrinsic ordering. It’s genuinely more natural to count the letter
"b"as coming “between” the letters"a"and"c"in"abc"than it is to count"c"as coming “between”"a"and"b", because of way the string"abc"is inherently structured.
Sometimes ordered pairs, triples, and so on — the general class of things I will call
n-tuples or just tuples — are referred to as “ordered sets.” Avoid this usage; it will be too confusing when we look at a different notion of ordered set, in a few classes.
Now we are going to talk about a notion where the label “ordered” can be taken more seriously. We saw above that one special category of binary relations on a set (those that are reflexive, symmetric, and transitive) are distinguished with the name “equivalence relation.” Other special categories of binary relations on a set are distinguished with the name orders. But here there are a couple of different patterns.
First off, there is a contrast between a partial order and a total or linear order. The general idea here is that with a partial order, not every pair in the relation’s domain needs to be comparable; with total/linear orders they do (at least, if they’re distinct objects).
Unlike with functions, where an unqualified “function” means “total function,” with order relations an unqualified “order” usually means “partial order.” Since an order relation is always defined on a set (the relation’s domain), we can describe the set together with that order relation as a partially ordered set (poset for short).
Second, there is a contrast between orders that are more like ≤ on the natural numbers, and ⊆ on sets, on the one hand, and orders that are more like < on the natural numbers, and ⊊ or ⊂ (the proper subset relation) on sets, on the other. The former are called weak or non-strict orders, and the latter are called strong or strict orders. When no qualifier is given, usually a non-strict order is meant.
There’s also a more specific usage of the label “weak order,” that only applies to some of these. So I will avoid that vocabulary, and use non-strict/strict instead.
Official definitions:
R is a non-strict partial order iff it’s transitive, reflexive, and anti-symmetric.R is a strict partial order iff it’s transitive, irreflexive, and anti-symmetric. (Being irreflexive and anti-symmetric is equivalent to being asymmetric.)If some distinct elements fail to be comparable by a relation, then it won’t be total/linear.
Examples:
⊆ is a non-strict partial order on this set, but merely partial: the elements {"a"} and {"b"} aren’t comparable (neither is a subset of the other).≤ on ℕ is a non-strict total/linear order.< on ℕ is a strict total/linear order.Consider the relation that holds between two strings when the length of one is no greater than the other. Let’s call this shorterOrSameLen. The string "a" stands in this relation to itself and also to "ab". But it also stands in this relation to the string "b", and "b" also stands in it to "a", though these strings aren’t identical to each other. So this relation is not anti-symmetric, and won’t count as a partial order. In some respects it’s like a partial order though. Relations like this are sometimes called preorders or quasiorders (and are sometimes represented using ≲).
Notation: if a text wants to talk about some arbitrary partial (or total) order, they’ll often represent it as ≤ or <. In those usages, these symbols aren’t interpreted to mean the familiar arithmetic relations of being less-than. If the first is used, the author clearly wants to talk about a non-strict order; if the second is used, they may want to talk about a strict order, or they may want to talk about a non-strict order. You’ll have to check the context to determine which. It’s easier if we use different notation to represent an arbitrary order relation. Sometimes authors use ≼ (or ≺ for a strict order), or ⊑ (or ⊏ for a strict order). I’ll use the last of these, as it’s easier to see the difference from ≤ and <.
If an author has specified some non-strict order ⊑, the corresponding strict order ⊏ can be defined as:
x ⊏ y =def x ⊑ y & ~(y ⊑ x)Given our focus on partial orders, this could equivalently be expressed as x ⊑ y & y ≠ x, but the definition above could also be used for pre/quasiorders.
If an author has specified some order ⊑, and then writes things like y ⊒ x, they’re using ⊒ to represent the inverse relation to ⊑: that is, y ⊒ x iff x ⊑ y. Similarly for ⊏ and ⊐.
Here is another kind of “completeness” notion on a relation: When a partial order R satisfies this property:
∀x ∀y (xRy ⊃ ∃u (xRu & uRy))then R’s domain is called dense with respect to that order. (This label could be used for either a non-strict or strict order.) The rational numbers and the real numbers are each dense with respect to the less-than ordering. “In between” any distinct rationals (or reals) there is another rational (real).
When we have a partially ordered set (that is, a domain with a partial order defined on it), we sometimes talk about “maximal” or “greatest” elements of the set when so-ordered. These aren’t the same, and don’t always exist. For example, there is no maximal or greatest element of ℕ ordered by ≤. But some sets have maximal elements, and they may have more than one. For example, if we use ⊑ to express the relation “is a prefix of,” and we consider the set of strings {"a","b","ab","aba","abb"}, then all three of "b", "aba", and "abb" are maximal with respect to that ordering, because there are no elements of the set (other than themselves) that they are prefixes of.
Officially:
m is a maximal element of partial order ⊑ on set Α =def ∀a ∈ Α (m ⊑ a ⊃ a ⊑ m)
Since partial orders are anti-symmetric, the consequent could also be expressed as a = m.
The idea of a greatest element is more specific. That has to be such that everything in the set stands in the ⊑ relation to it. Officially:
g is a greatest element of partial order ⊑ on set Α =def ∀a ∈ Α (a ⊑ g)
In our previous example with “is a prefix of,” there is no greatest element.
A set can have at most one greatest element (wrt a given partial order ⊑) and any greatest element will be maximal (wrt that order). A set can have a single maximal element but no greatest element: consider the set {"b","a","aa","aaa",...} ordered by “is a prefix of.”
If an order is total/linear, any maximal element must be greatest.
The notions of “minimal” and “least” elements are defined analogously.
The definitions of maximal and greatest can also be used for pre/quasiorders. With these, a greatest element need not be unique. For example, a set of people may have more than one member who are greatest in height (that is, at least as tall as everyone else). With partial orders, there cannot be ties of that sort. The anti-symmetry of a partial order means that any x,y where x ⊑ y and y ⊑ x must be equivalent. So with partial orders, if there is a greatest element, it must be unique; and it will be the only maximal element. But as we saw a moment ago with the ordering of {"b","a","aa","aaa",...} by “is a prefix of,” a unique maximal element needn’t be greatest.
Every pre/quasi- or partial ordering of a finite domain must have some maximal and some minimal elements. (Some elements may be both.) These need not be unique, because some elements of the domain may be incomparable. But if the order is weakly-connected (so total/linear), the maximal element(s) will be greatest and the minimal element(s) will be least.
With infinite domains, there may be no maximal elements, or many, or just one but it not be greatest (as we saw), or some maximal elements all of which are greatest. As we said, in the case of partial orders (which have to be anti-symmetric) for the last option there can be only one such; but for pre/quasiorders there may be several.
When the greatest and/or least elements of a poset exist, they are sometimes called top or ⊤ or one and bottom or ⊥ or zero. The symbols ⊤ and ⊥ are also used in other ways, and of course the words “zero” and “one” are commonly used to refer to familiar elements of ℕ, which need not be the bottom or top of particular partial orderings they belong to.