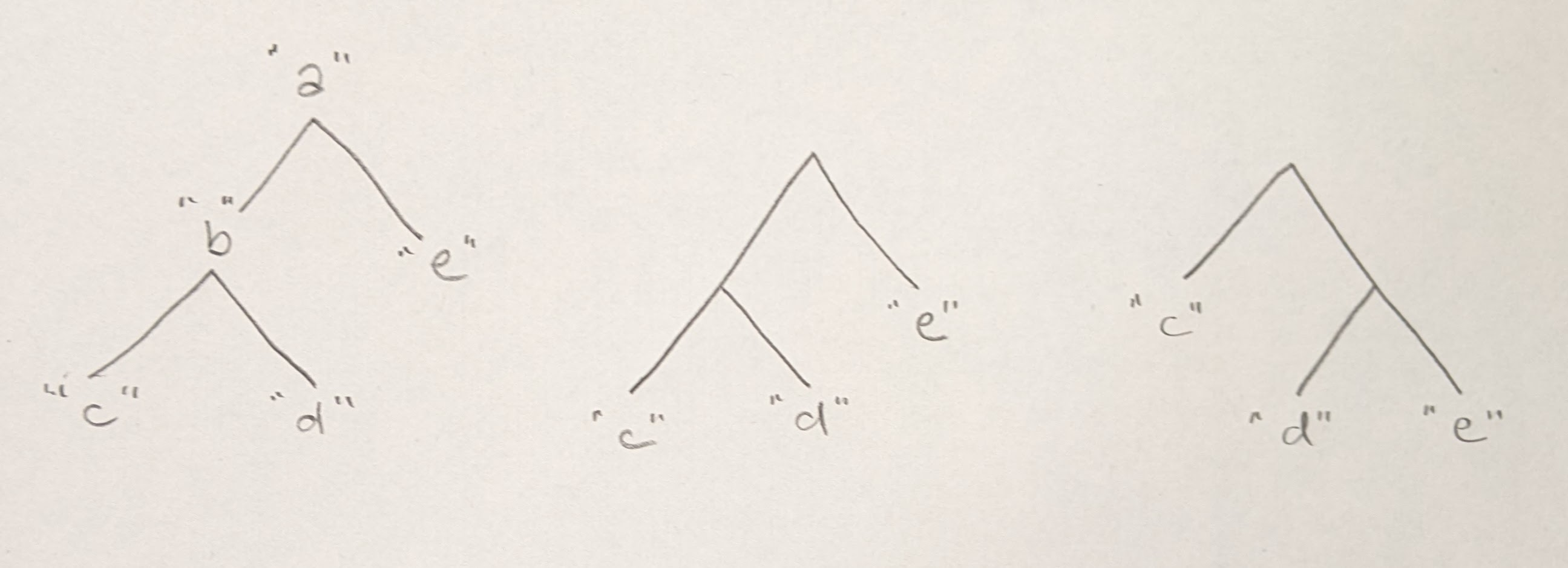
Strings/finite sequences are one way in which elements can be structured or organized. At the end of our last class, I mentioned the idea of “trees,” which is another way in which elements can be structured. We’ll talk about these in detail in later classes. But the intuitive idea is that here are some trees:

The elements that are structured by, or occupy/annotate/label positions in these example trees are strings. But as with sequences and other structures, the elements can be other types of things too (numbers, planets). Sometimes the trees have all of positions occupied, as in the leftmost example. Sometimes only their “leaf” positions are occupied, as in the two rightmost examples. (In computer applications, sometimes only the “inner” positions, occupied by the strings "a" and "b" in the leftmost tree, are occupied.)
Note that the middle example and the rightmost example are distinct trees, because they structure their elements differently.
I suggested at the end of class thinking about what conventions we might use if we wanted to encode these tree structures into a single string, in the way that we were talking about encoding sequences into a single string.
One way to encode the leftmost tree would be like this (with the string displayed on the next line):
((c b d) a e)(That’s the same as "((c b d) a e)". When I display a literal string, I omit the surrounding quotes.)
We’ll be using an encoding like that later in the course, with "b" and "a" replaced by logical connectives like "∨", "&", or "⊃".
In Linguistics a different convention is used. They’d represent the middle tree like this:
[ [ c d ] e ]And the rightmost tree like this:
[ c [ d e ] ]If they’re working with trees like the leftmost one (as they often do), they’d represent it like this (notice the subscripted "a" and "b"):
[a [b c d ] e ]
Generally, they have labels for syntactic categories like “DP/NP” or “VP” or “S” in place of "a" and "b", and natural language words or phrases in place of "c", "d", and "e".
The language we’ve introduced for talking about strings doesn’t include formatting choices like subscripting, so we can’t encode trees in exactly that way. But if in some contexts we were always going to be working with trees like the leftmost one, we could just use:
[a [b c d ] e ]and understand the first word after an opening [ as if it were subscripted in the linguist’s notation. Or if we were sometimes going to be working with trees like the leftmost one, and sometimes like the other two, we might take a special letter "*" which didn’t have any other role, and represent the middle tree like this:
[* [* c d] e ]That doesn’t represent a tree like the leftmost one but where the "a" and "b" positions are occupied by the "*" letter; rather it represents a tree where those positions are unoccupied.
As I said, we’ll come back to talk about trees in more detail later. This is just to get a feel for how we might have conventions for various ways of using single strings to encode or represent structures of other strings.