Phil 455: Homework 4 (on Lattices and Algebras)

Since this homework was posted late, it won’t be due until the end of the day (11:59 pm) on Friday.

Examples 2 and 3 on the lattice webnotes were:

Example 2

0 ⊏ 2 ⊏ 4 ⊏ ... ⊏ 1 ⊏ 3 ⊏ 5 ⊏ ...

Example 3

0 ⊏ 2 ⊏ 3 ⊏ 4 ⊏ 5 ⊏ ... ⊏ 1

These are just suggestive representations of the two orderings. Specify them each more rigorously, by saying something of the form “the graph of the first relation is {(x,y) ∈ ℕ² | blah-blah}.”
Consider the order relation on elements of ℕ² whose graph is {((x,y),(x′,y′)) | x ≤ x′ and y ≤ y′}, where ≤ is the familiar less-than relation on ℕ. Is this order relation total (that is, weakly connected)? Is it well-founded? Justify your answers.
For any set Β, consider the partial ordering of 𝟚^Β by ⊆. (a) Will any two elements Γ, Δ of that domain have a join, and if so, what is it? (b) Will they have a meet, and if so, what is it? (c) Does this partial ordering count as a lattice? If so, say whether it has a top and/or bottom element.
Consider the following diagrams of posets (with a ⊏ b being represented by a being below b and connected by an always-upwards path). Which of these posets are lattices?
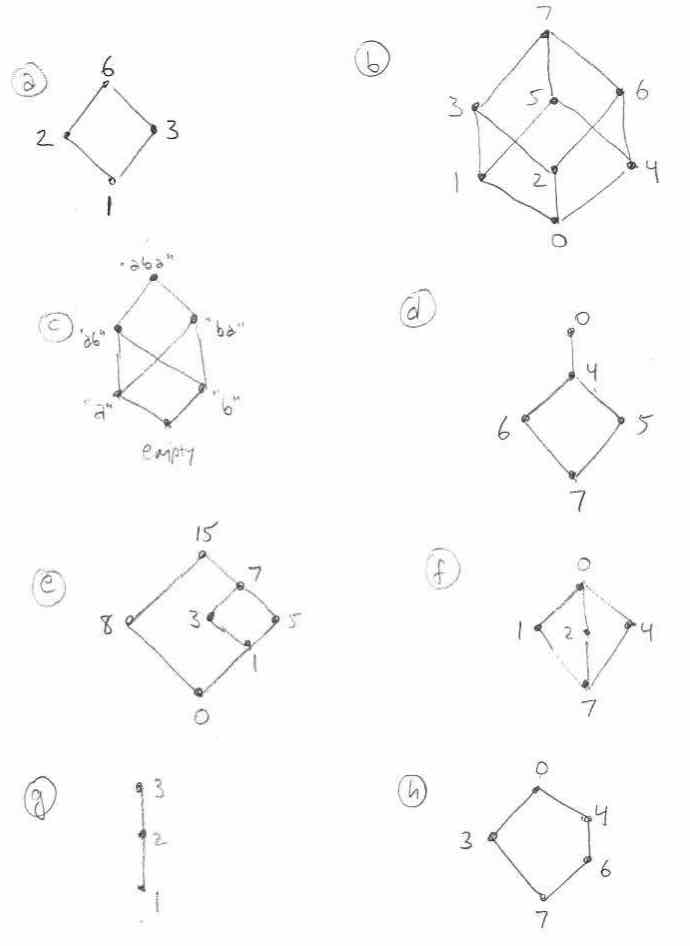
Consider the set of strings S {empty,"a","b"}. Let T be its closure under concatenation (^). (Earlier we only explicitly talked about closing sets under binary relations, but I trust the extension to binary operations, which can be understood as ternary relations, will be intuitive.) Is concatenation an operation on S? Is it an operation on T? Does the algebra consisting of T and concatenation form a monoid? Do any members of that algebra have inverses?
In Example 12 of the lattice webnotes, we considered the set of all strings formed from the letters "a" and "b", ordered by the relation of being a substring of. We said that that ordering was well-founded, but not total. Consider the following, alternative ordering of these strings, which is total:

string xs ⊏ string ys =def string ys is non-empty, and either: a. xs is a prefix of ys; or b. there are (possibly empty) strings us, vs, and ws such that: xs = us ^ "a" ^ vs and ys = us ^ "b" ^ ws.

Thus by this ordering: "a" ⊏ "aa" ⊏ "aab" ⊏ "ab" ⊏ "b".

This is called the lexicographic ordering of the strings, as it’s based on the way dictionaries order words. Prove that this ordering is not well-founded.

(Hint: try to add more elements into the example ordering between aa and aab.)
This problem makes use of the function mod that you met in Homework 3 problems 6–7. We’ll talk about “addition mod n,” which is the binary function from (x,y) to (x+y) mod n, and “multiplication mod n,” which is the binary function from (x,y) to (x⋆y) mod n. You can help yourself to the fact that each of these functions is commutative and associative.
1. Show that addition mod 4 is an operation on the domain {0,1,2,3}, and that the algebra consisting of that domain and operation forms a group.
2. Show that multiplication mod 7 is an operation on the domain {1,2,3,4,5,6}, and that the algebra consisting of that domain and operation forms a group.
1. Show that multiplication mod 11 is an operation on the domain {1,3,4,5,9}, and that the algebra consisting of that domain and operation forms a group.
In Homework 2 problem 9 you met the “symmetric difference” operator on sets, which we symbolized as ⊕. Α ⊕ Β was defined as (Α ∪ Β) – (Α ∩ Β), and you proved this was equivalent to (Α – Β) ∪ (Β – Α).
1. In Homework 2 problem 14, you argued that for any set Β, ∪ and ∩ and – are operators on 𝟚^Β. Why does that entail that ⊕ is also an operator on 𝟚^Β?
2. Use the second fomulation of Α ⊕ Β to prove that ⊕ is commutative. You can help yourself to the fact that ∪ is commutative.
It’s fine if you want to use + or (+) or xor to represent symmetric difference, rather than ⊕.
Here is the outline of an argument that ⊕ is associative.
- Α ⊕ Β consists of those elements that are in exactly one of Α and Β: they’re in Α but not Β, or Β but not Α.
- So (Α ⊕ Β) ⊕ Γ will consist of those elements that (i) are in Γ but not Α ⊕ Β, or (ii) in Α ⊕ Β but not in Γ. Case (ii) can be rephrased as “the element is in exactly one of Α and Β, and not in Γ.” Case (i) subdivides into (ia) the element is in Γ but in neither of Α or Β; or (ib) the element is in Γ and in both of Α and Β. Cases (ii) and (ia) can be combined as “the element is in exactly one of Α, Β, and Γ.” Case (ib) can be rephrased as “the element is in all three of Α, Β, and Γ.” Hence, (Α ⊕ Β) ⊕ Γ consists of those elements that are either in exactly one, or in all three, of Α, Β, and Γ.
- Α ⊕ (Β ⊕ Γ) also consists of those elements that are either in exactly one, or in all three, of Α, Β, and Γ; because …
- Since these conditions are the same, ⊕ is associative.
Complete the argument by filling in the … You may want to help yourself to the fact you proved in problem 8b.
(a) Does the ⊕ operation have an identity? (b) Does every element of 𝟚^Β have an inverse for the operation ⊕? What is it?
Given the facts shown in problems 8–10, what category does the algebra consisting of the domain 𝟚^Β and the ⊕ operation belong to?
In Homework 2 problem 15 you worked with a set Ψ of all bijections on another set Β. You argued that function composition (∘) is a non-commutative operation on Ψ. We also know from Homework 2 problem 16 that function composition is associative. Given what you established in Homework 2 problems 17 and 18, what category does the algebra consisting of the domain Ψ and the ∘ operation belong to?
Consider the “checkerboard game” defined as follows. There’s a checkerboard with four squares, which I’ll name NW, NE, SE, and SW. A single checker is located on one of the squares. It can move either vertically (from NW to SW, or from SW to NW, and so on), or horizontally (from NW to NE, or from NE to NW, and so on), or diagonally (from NW to SE, or from SE to NW, and so on). Or it can stay in place. Consider the set consisting of these four moves {vertical,horizontal,diagonal,stay}. Consider the operation of performing two of these moves in sequence: vertical∙horizontal means first move horizontally then move vertically. (We order the moves in the same way we order functions when describing their composition.)
1. Here is an argument that the ∙ operation is associative: a move can be understood as a f__ from s__s to s__s, and we’ve already shown that f__ c__ is associative. Fill in the blanks.
2. Prove that the set of moves described together with the ∙ operation form a group.