Digraph #1
A graph is a mathematical structure consisting of 1 or more (but finitely many) vertices or nodes, on the one hand, and 0 or more edges joining two vertices, on the other. There are several different variations on this idea.
In a simple graph, the edges have no direction; in directed graphs or digraphs, they do. In the latter case the directed edges are sometimes called arrows or arcs.
In simple graphs and simple digraphs, it is usually forbidden for an edge to join any vertex to itself. For some applications, though, it is useful to allow graphs that permit that. (Consider the next-state diagrams for finite automata that we were just recently working with.) When such edges are allowed, they are called self-loops or just loops, and sometimes the graphs that include them are called pseudographs.
In simple graphs and simple digraphs, it is usually forbidden for more than one edge to join two vertices (in the same direction: a digraph is allowed to have a directed edge from \(v_1\) to \(v_2\), and then another directed edge from \(v_2\) to \(v_1\)). For some applications, though, it is useful to allow graphs with multiple edges between some pairs of vertices; sometimes these are called multigraphs. (For example, the famous Bridges of Koenigsberg problem, which launched the discipline of graph theory, makes use of multigraphs rather than simple graphs.)
As is implicit in the above explanations, a graph can have many vertices but no edges at all. Or it may have edges connecting some proper subsets of its vertices, but have several disconnected "pieces." We'll introduce some terminology to describe this more carefully below.
In some applications, it is permitted for there to be edges that "hang free," instead of always joining a pair of vertices. They lack a vertex on one of their ends. (Sometimes even on both ends.) We won't be discussing graphs of this sort, though; nor will we be disussing multigraphs or pseudographs more than we already have.
Consider a simple (undirected) graph, and let a walk be a sequence of adjacent vertices, perhaps visiting the same vertex several times, perhaps even traversing the same edge several times. There is a variety of terminology for different restrictions on this notion. We will say a path is a walk of 1 or more vertices, where (as in any walk) successive vertices in the sequence are adjacent, and (now we impose special restrictions) no vertex (and thus no edge) is visited more than once, with the exception that the ending vertex is allowed to be (but needn't be) identical to the starting vertex. A closed path, where the start and end vertices are the same (and the path traverses at least one edge), is called a cycle. A path of length 0 would just be a single vertex. Any single edge would give us a path of length 1. Paths of length 2 would include 2 edges; and so on.
Recall the notion of a self-loop, discussed before. If those are allowed, they would count as cycles (on our definitions). They would be cycles of length 1. But there can be longer cycles too. In a non-multigraph, where at most a single edge joins any two vertices, the shortest cycle which isn't a self-loop would have length 3. Although it's common to prohibit self-loops from the graphs one is talking about, it's on the other hand common to allow longer cycles. For some purposes, though, it is useful to prohibit cycles too, and only consider acyclic graphs.
The components of a simple (undirected) graph are the maximal subsets of vertices such that for every pair in the set, there is a path between them (together with all the edges joining those vertices). When a graph has only one component --- that is, when there's a path between any two vertices in the graph --- then the graph is called connected. (Graphs are complete when there is, more demandingly, an edge between any two vertices.)
A component of a graph is an example of a more general notion, that of a subgraph. A subgraph of a graph \(G\) would be given by any subset of \(G\)'s vertices, joined by some subset of the edges that join those vertices in \(G\). \(G\)'s components are its maximal connected subgraphs: that is, subgraphs of \(G\) that are connected and aren't proper subgraphs of any other connected subgraphs of \(G\).
When we consider the question whether graph \(H\) is a subgraph of \(G\), or whether it is equivalent to \(G\), we ignore the specific identities of the vertices. Graphs count as equivalent so long as there is some isomorphism between them that preserves the relevant edge structure. And to count as a subgraph of \(G\), \(H\) doesn't have to contain any of the same specific vertices as \(G\) does; it's enough that there is a (homo)morphism from \(G\) to \(H\) that preserves the relevant edge structure.
Deep issues in the philosophy of math lurk here. Ideally we'd like to think of a graph \(G\) in a way that's independent of any choices about which specific objects are the vertices. Mathematically, a graph should just be a pattern by which any set of so-many vertices may be joined. But we won't dig into these issues here.
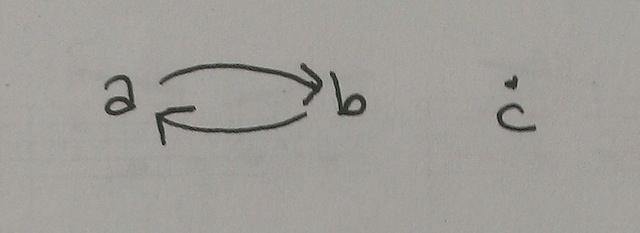
When it comes to digraphs, there are several different notions of connectedness. It's clear that a digraph like this one is unconnected, in every sense:

Digraph #1
On the other extreme, it's clear that a digraph like this one is connected, in the most robust sense. Every pair of vertices is joined by a path (in both directions, in fact), which always travels "with" the direction the digraph's arrows. This is called a strongly connected digraph.
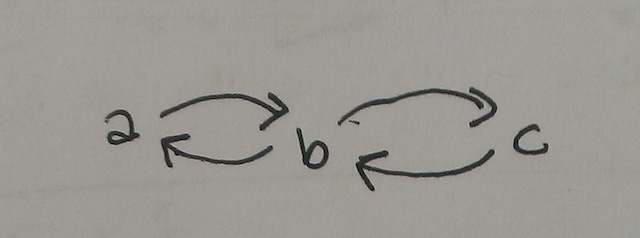
Digraph #2
But between these extremes there are different kinds of digraphs that are kind-of, sort-of, in-a-way connected. For example, in this digraph:

Digraph #3
for any pair of vertices you choose, you can always find a path that travels "with" the direction of the digraph's arrows, but sometimes this path will only go from the second vertex to the first, and not from the first to the second. There is a path of this sort from \(a\) to \(c\), but not one from \(c\) to \(a\).
The following two digraphs are connected in an even weaker sense:
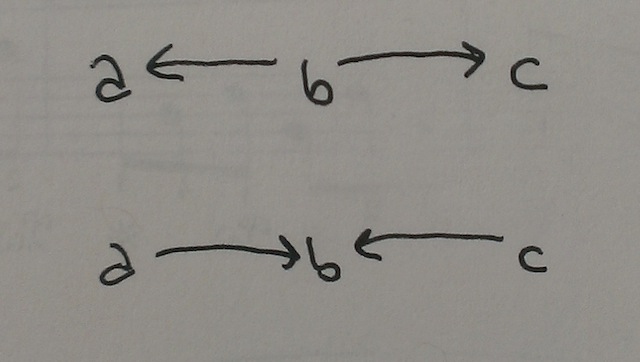
Digraphs #4
In these cases we cannot find a path that travels only "with" the direction of the arrows either from \(a\) to \(c\) or from \(c\) to \(a\). Unlike Digraph #1, though, at least in this case there is a kind of path between \(a\) and \(c\). It just requires sometimes traveling "with" the direction of an arrow, and sometimes traveling "against" it.
These are all legitimate notions of connectedness and of a path. Henceforth, though, when I speak of a directed path from \(c\) to \(a\), I shall mean only the kind of structure we see in Digraph #2.
There are natural correlations between (non-multi)graphs and relations. One way to think of this would associate the holding of the relation with the presence of an edge. Then, when we have a simple graph that excludes self-loops, the relation would have to be irreflexive. When the relation is symmetric, we could think of it as correponding to either an undirected graph, or to a digraph that just happens to also have a reverse arrow wherever it has an arrow. When the relation is not symmetric, we should understand the graph to be directed.
A different way to correlate graphs and relations would associate the holding of a relation not with the presence of an edge but the presence of a path. This makes sense when the relation is reflexive and transitive. Then the relation holds between \(v_1\) and itself iff there's a path starting with \(v_1\) and ending with \(v_1\)---and there always is such a path, of length 0. (We don't need to rely on the "self-loopy" paths of length 1.) It holds between \(v_1\) and \(v_2\) if there's a (directed) edge joining \(v_1\) to \(v_2\), or a (directed) edge joining \(v_1\) to \(\dots\) to \(v_2\). If the relation fails to be symmetric, we should here also understand the graph to be directed.
There are also interesting correlations between graphs and groups, in both directions. But this would take us too far afield.
The presence or absence of an edge between two vertices carries a single bit of information about how those vertices are related. Sometimes we want to use graphs to represent richer information. For example, we might be using the vertices to represent cities, and want to associate with the edges information about how far apart those cities are. We can do this by just adding to our graph a function from edges into whatever kind of information we want to work with. Graphs with labeled edges of this sort, especially when the labels are real numbers, are sometimes called networks.
For some purposes, we might also (or instead) want to have labels for vertices. Why might we want to do that? Whatever we were tempted to use as the label for some vertex, couldn't we just let that thing be the vertex? For example, if we're graphing distances between cities, can't we just let the cities themselves be our vertices? Why do we need to have some separate set of vertices, that the cities merely label?
Well, in some situations it will be fine just to let the objects you're interested in constitute your vertices. But if there is ever the prospect of wanting one and numerically the same object to simultaneously occupy two different positions in your graph, then you can't do that. Numerical sameness and difference between the vertices is what constitutes sameness and difference of graph positions. So it makes no sense to have two positions constituted by what is numerically just a single object. On the other hand, it would be completely unproblematic to let one and numerically the same object simultaneously be the label for two distinct vertices.
But, you may ask, would such a need ever arise?
Well, suppose we are making a syntax tree of a sentence where the same word appears multiple times. A syntax tree is a kind of graph, which we'll look at more closely in a moment. So now if we think that what gets associated with the vertices of this graph are the word-types of the relevant sentence, this would be a case where we'd want to associate the same object (a given word-type) with multiple vertices.
You might protest: why don't we these trees as inhabited by word tokens instead of word types? Then we can be sure that when "the same" word appears multiple times in the sentence, there will always be multiple tokens. And we can let those tokens be the vertices, rather than having them label some separate set of vertices.
I'm afraid that strategy will not work in general. Consider the following inscription of the sentence \(Stupid~is~as~stupid~does.\)
| Stupid |
is as does. |
Given the most natural understanding of the notion of a token, this inscription only contains a single token of the word-type \(stupid\). Yet that word should occupy two different syntactic positions. Some philosophers will respond to this by distinguishing by what I'm here calling a token, and what we might call an occurrence. Even if the above inscription has only one token of the word-type \(stupid\), they'd say, that word-type nonetheless has two occurrences in the sentence. (Some philosophers even insist that that's what they mean by "token." This surprises me, but ok.)
Now I have no objection to this notion of an occurrence. But I think this occurrence-talk is just another way of expressing the idea of a single word-type being associated with distinct syntactic positions. The two occurrences aren't given to us in advance, in such a way that we could use them to build the two positions or vertices. The distinctness of the occurrences instead already assumes the distinctness of the positions. And that's just what I'm recommending. We should think of the words --- it could just be the word-types, there's no need to invoke tokens here --- as labeling distinct vertices or positions in the syntax tree. There is no obstacle to one and the same word labeling multiple vertices, because the label doesn't constitute the vertex, it's just associated with it.
As we go on in class, we'll several times make use of the notion of a tree. There are three different ways of getting to this notion.
One way starts from the notion of a simple undirected graph. Any graph without cycles can be called a forest, and a connected forest --- that is, a forest with just one component --- can be regarded as a tree. In such graphs (and only in them), there will be exactly one path between each pair of vertices. Any of the vertices can then be chosen to play the special role of the tree's root, and the selection of the root will impose an ordering on the rest of the vertices, tracking the directions towards / away from the root. For example, in the following graph:
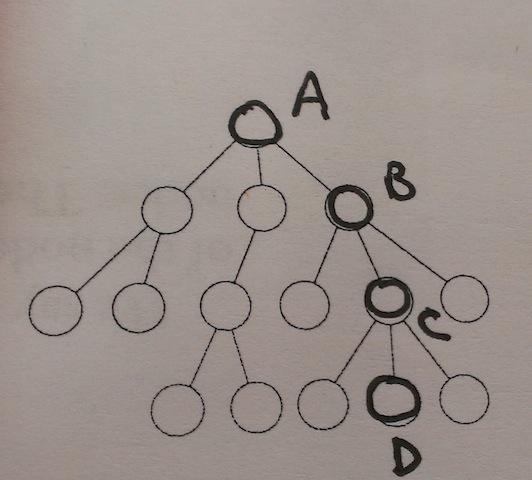
Tree #3
as I said, any of the vertices could be selected as the root, but if we select \(A\) as the root, then relative to vertex \(C\), \(B\) will be closer to the root and \(D\) will be farther away. Any vertices of degree 1 (that aren't themselves the root) are called the leaves of the tree. Vertices that aren't the root and aren't leaves are called interior vertices.
A different strategy wouldn't impose an order onto a tree by designating a root, but would instead start with digraphs that already have an order. Not every digraph could constitute a tree, but for those that do, the root would just be the vertex that doesn't have any incoming arrows.
A third strategy for getting a tree will emerge below.
Given a tree-like structure via one route or another, we can say that one vertex dominates another vertex if there is a path leading from the second, through the first, going towards the root of the tree. (We also count vertices as dominating themselves.) Here's an example:
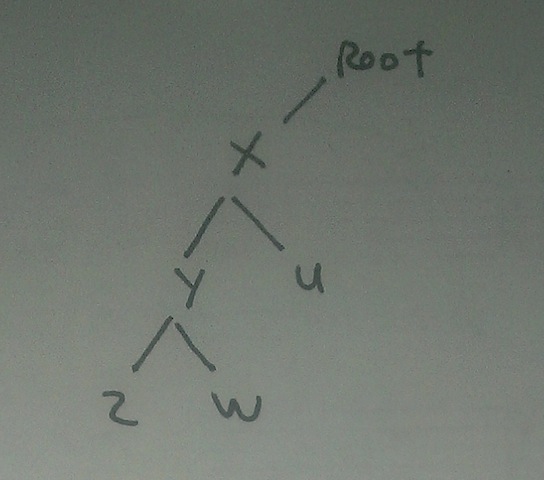
Tree #4
In this tree the vertex \(x\) dominates all of the following vertices: \(x\), \(y\), \(z\), \(w\), and \(u\). The dominating relation is reflexive, transitive and anti-symmetric, and thus counts as what we'll later call a non-strict partial order. Just to fix ideas, another example of a relation of that sort is the \(\se\) relation on sets.
The root vertex in a tree is not dominated by any vertex but itself. The leaf vertices in a tree do not dominate any vertex but themselves.
When we diagram a tree on paper, the diagram may end up having geometrical properties that aren't any part of the mathematical structure we're diagramming, but are just artifacts of our particular drawing. For example, the right-left relations in graphs we diagram generally are just accidents of our drawing. But one can if one wishes impose an ordering on the edges leaving each vertex. When using trees to represent syntactic structures, we do in fact do this. We call this ordering preceding, and by convention we will respect it in the left-right structure of the tree diagrams we draw. So if the Tree #4 diagram above is understood to have its edges ordered in this way, then we'll say that vertex \(y\) precedes vertex \(u\), and vertex \(z\) precedes vertex \(w\). It is useful to think of "child" vertices as inheriting the precedence relations of their parents, so that we can say that vertices \(z\) and \(w\) both precede vertex \(u\) as well. We will want to rule out cases like this:
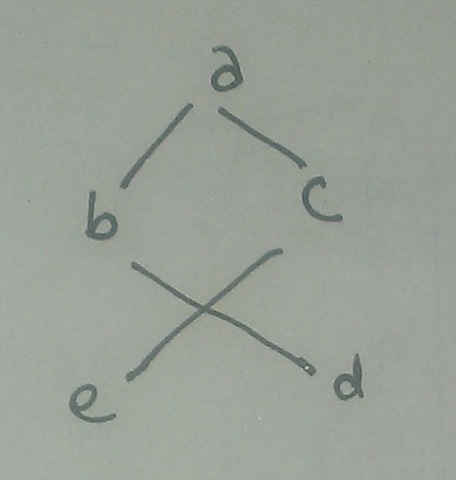
Tree #5
We can do that by saying that if \(b\) precedes \(c\) then all nodes dominated by \(b\) have to precede all nodes dominated by \(c\).
Whereas a good model for the dominating relation is \(\se\), the precedence relation is instead usually thought of like \(\subset\). We don't allow vertices to precede themselves.
We've described how a dominating relation can be read off of a rooted tree, and how a precedence relation can be added to such a tree. A different way to go is to take the dominating relation and the precedence relation as given, and to let the tree in question be implicitly specified by them. This is what Partee does in the reading, when she introduces the notion of a constituent structure tree. (And this is what I earlier called a "third strategy" for getting a tree.)
However we get to a tree with a dominating and precedence structure, we define the fringe or yield of the tree to be the sequence of labels associated with the tree's leaves, in their left-to-right precedence order. So the fringe of this tree:
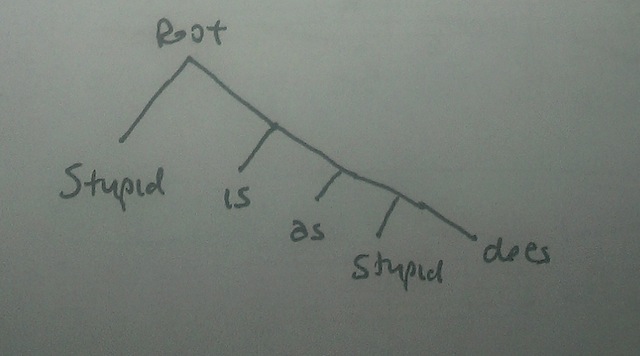
Tree #7
would be the sequence \(Stupid\), \(is\), \(as\), \(stupid\), \(does\).