In class discussion, I introduced the 0-tuple \(()\), which is the sole member of the type that may be written as \(1\) or \(e^0\), where \(e\) is any type. In some programming languages or type-theory formalisms, this object \(()\) has an important role. In other programming languages and formalisms, it has no role at all and can't even be expressed. When theorists do work with this object, they usually call it unit or void.
In conversation with Rosa and Kyle after class, it emerged that there are two ways of talking about functions whose domain is \(1\), the type for which \(()\) is the sole member.
It becomes easiest to understand these if we first think about two ways of talking about functions whose domain is \(e^2\), for some type \(e\). On the one hand, you could say such functions "take two arguments." On the other hand, you could say that such functions take a single argument, which is a kind of aggregate or container with two constituent elements.
Ok, paralleling that are two ways to talk about functions whose domain is \(1\) (or \(e^0\)). You could say such functions "take no arguments," they simply have a result. On the other hand, you could say that such functions take a single argument, which is a kind of aggregate or container with no constituent elements.
Perhaps these are in the end two different ways of articulating what is fundamentally a single concept. Or perhaps they in the end express two different ideas, and it's objectionable to slip back and forth between them. I don't want to try to settle that here. I just will allow myself to slip back and forth between these ways of talking, and if it turns out later I was doing something bad we'll have to come back in time and scold me.
In the page on automata, I use some shorthand like this: \([_{\mathrm{Q}} \: x \: y]\) to represent a tree. Here are two photos of what that shorthand looks like when unpacked into a more tree-looking form.

Tree #1
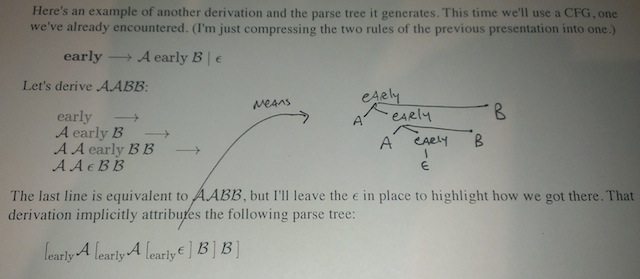
Tree #2
The next homework exercise requires you to show the parse trees for an expression on two different grammars. Here's how you can show me your work. The best solution will be to draw it on paper and put the paper, with your name on it, in my mailbox. Second-best will be to use the same shorthand I did above. The third-best will be to draw it on paper and take a picture with your phone and email the picture to me.
So the string we want to generate is: \(x-y-z\). Here is the first grammar:
\(\mathrm{term} \longrightarrow x \mid y \mid z\)
\(\mathbf{complex1} \longrightarrow \mathrm{term} \: ( \: \boldsymbol{-} \: \mathrm{term} \: ){*}\)
Here is the second grammar:
\(\mathrm{term} \longrightarrow x \mid y \mid z\)
\(\mathbf{complex2} \longrightarrow ( \: \mathrm{term} \: \boldsymbol{-} \: ){*} \: \mathrm{term}\)
Neither of these grammars is more correct than the other. However, perhaps you can see how, when we take the parse tree generated by the one of the grammars, and feed it into our semantic processor to evaluate it, it'll just naturally be evaluated as though the string were grouped like this: \((x-y)-z\). That is in fact the conventional way to understand \(x-y-z\). On the other hand, when we take the parse tree generated by the other grammar, and feed it into our semantic processor to evaluate it. unless we watch what we're doing, we might inadvertently end up evaluating it as though the string were grouped like this: \(x-(y-z)\). And that would be wrong, or at least unconventional. The parse tree generated by this other grammar doesn't force us to semantically evaluate it in that way. But it might take some thought or work on our part to evaluate that parse tree so as to get the same result as we'd get from \((x-y)-z\). The final part of this homework exercise is to say which of the two grammars above matches each of the descriptions given in this paragraph.
Summarizing: HOMEWORK EXERCISE 53 is: (a) write the parse trees for \(x-y-z\) for each of the two grammars given above; and (b) say which parse tree most naturally invites, or is most hospitable to, being interpreted as \((x-y)-z\), and which as \(x-(y-z)\). Explain your answers.
Just for fun. Is every \(\mathbf{sentence}\) produced by the following grammar a well-formed and meaningful sentence of English?
\(\mathrm{noun} \longrightarrow {\color{blue}{fish}} \mid {\color{blue}{fish}} \: \mathrm{noun} \: {\color{blue}{fish}}\)
\(\mathbf{sentence} \longrightarrow \mathrm{noun} \: {\color{blue}{fish}} \mid \mathrm{noun} \: {\color{blue}{fish}} \: \mathrm{noun}\)
In class, I explained how if you had a Turing machine A that could enumerate the members of some set, and a Turing machine B that could enumerate the non-members, then you could make a Turing machine C that could eventually give you a definite and correct yes-or-no answer as to whether any given argument is in the set. This turned on the possibility of having Turing machine C emulate the behavior of Turing machines A and B. As I explained in class, machine C can emulate the running of machine A for a few steps, then switch and emulate the running of machine B for a few steps, then switch back to A, and so on. Eventually the argument we're interested in will show up in one of the lists being generated by machines A and B, either A's members-list or B's non-members list, and at that point machine C could stop and give its answer, yes or no.
I also wanted to explain, but didn't have time to, how if you have a Turing machine D that will eventually give a yes-answer whether any given argument is in a set, you could make a Turing machine E that could enumerate all the members of the set, albeit not in a order that you could usefully specify in advance. We don't assume that D is guaranteed to stop and answer no when the answer isn't yes; perhaps in those cases D never stops. To get our machine E, we have to first be able to enumerate all the possible arguments that D could be asked about. If we're using Turing machines to judge whether strings over an alphabet \(\Sigma\) belong to some language, the possible arguments will be all the infinitely many members of \(\Sigma*\). Those are easy to enumerate: we first list \(\varepsilon\), then we list all the strings composed of one letter, then for each string of one letter, we list all the ways of continuing it with one more letter, and so on. (If our alphabet had infinitely many letters in it, we'd have to use a somewhat different strategy or we'd never get around to listing strings of length 2. But for now we assume our alphabets are finite.)
Ok, now that we know how to enumerate the possible arguments for machine D, here's how E will work. It will generate the first possible argument for D, then emulate the running of D on that argument for a few steps. If that emulation hasn't yet finished, it will pause it, then generate the second possible argument for D, and emulate the running of D on that argument for a few steps. If that emulation hasn't yet finished, it will pause it, then emulate running a few more steps of running on the first argument. Then pause, generate the third possible argument, and emulate running on that argument for a few steps. Pause, continue the emulation on the second argument for a few steps, pause, continue the emulation on the first argument for a few steps. And so on.
Whenever any of our emulations stops with a yes answer, we can output that emulation's argument as one of the members of the set we're trying to enumerate. Since we assume machine D can be relied on to always eventually stop and answer yes when the answer is yes, there will eventually come a time when we get around to adding each argument that gets a yes-answer to the enumeration we're generating.